Common fastener components and standards
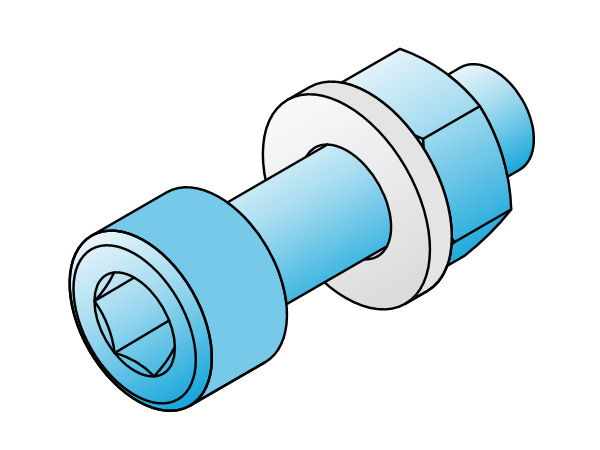
Introduction Below a table that contains commonly used fasteners sorted by fastener category. For precision engineering, commonly used fastener materials are stainless steel, brass or titanium. For applications in vacuum / cleanroom environments, fasteners that are polished, kolsterised and cleaned are recommended. Polished for reducing friction and particles, kolsterised (which is a surface hardening process) […]
Preferred fits
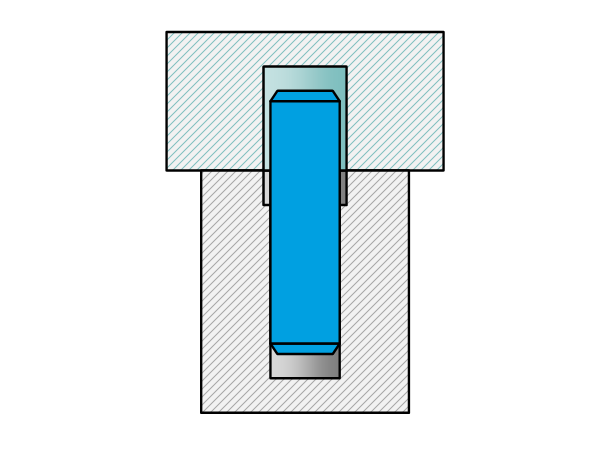
Preferred fits The table below shows the preferred fits according to ANSI B4.2-1978 with its overlap with the preferred fits of ISO 286-1 (2010) marked in green. Fits on shaft basis are preferred because of the availability of h6 dowel pins. For precision mechanisms G7/h6 is generally used as H7/h6 has a risk of getting […]
Static balancing
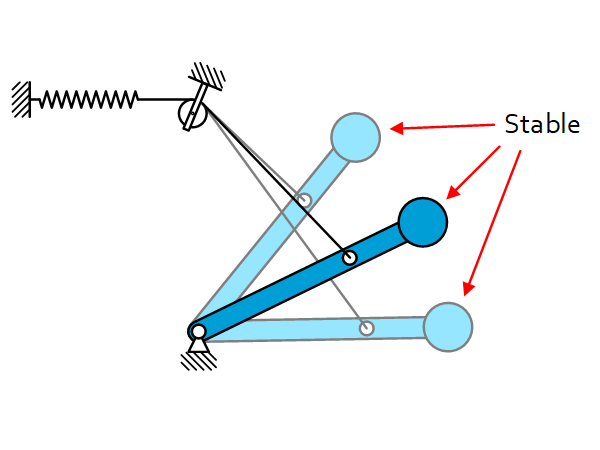
Introduction Statically balanced mechanisms are used to compensate for the gravity force of masses. Allowing these mechanisms to move from one configuration to another without the need for large actuation forces. This gravity compensation is done by using springs. Static equilibrity equation To have a static equilibrium the sum of all forces has to be […]
Equivalent stiffness
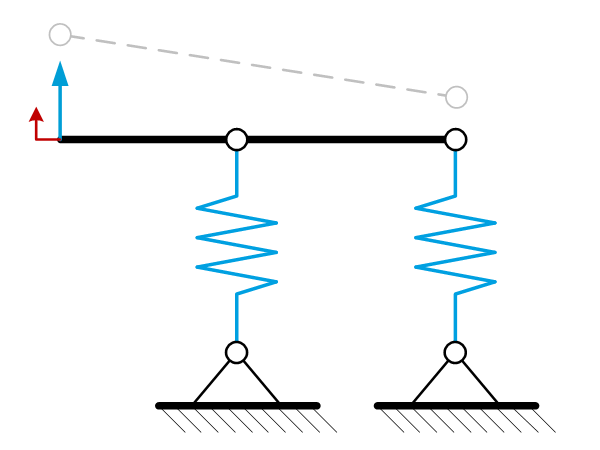
Introduction In many applications it is relevant to know the total connection stiffness of an object in relation to a given reference. In many cases there are several stiffness paths which introduces the need to calculate the ‘equivalent’ stiffness. This is a single stiffness representing the sum of all individual stiffness’ in the appropriate way, […]
Spring shapes

Introduction Various shapes can be used as a spring to provide certain stiffness. Below several shapes are described. Also the stroke according to the maximum occurring stress in the particular shape is added; maximum stroke at yield stress.$$tau_{0.2}approx0.4cdotsigma_{0.2} textsf{ (JPE estimate for metals)}$$ Below materials are characterized with: $E,sigma_{0.2},nu$
Cross spring pivot

Introduction Cross spring pivots are an interesting alternative for common flexure pivots in case transverse loads of the pivot are relatively high. The layout of a cross spring pivot can be chosen to optimize for large angular motion, or for optimal pivot behavior which is unbiased with parasitic displacements. Stiffness To get an idea of […]
Triangular body supported by tangential struts
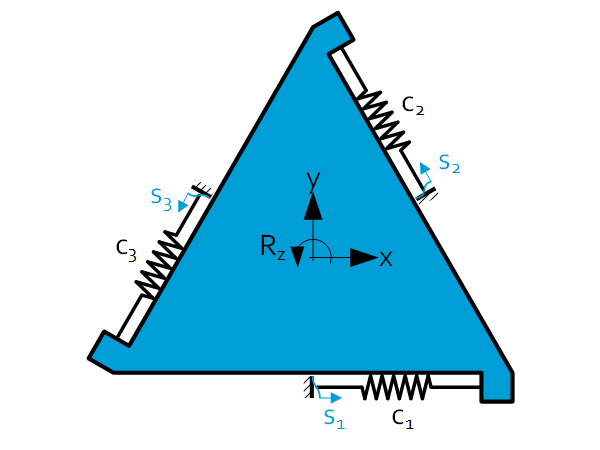
Introduction In many precision engineering solutions, flexure design with a frame configuration is used, where an equi-triangular body is supported by three tangentially oriented struts, to provide motion in $x$, $y$ and $R_z$. This sheet provides formulas for stiffness and displacement of the main body as function of the individual stiffness’s and displacements of the […]
Flexure hinge or elastic hinge
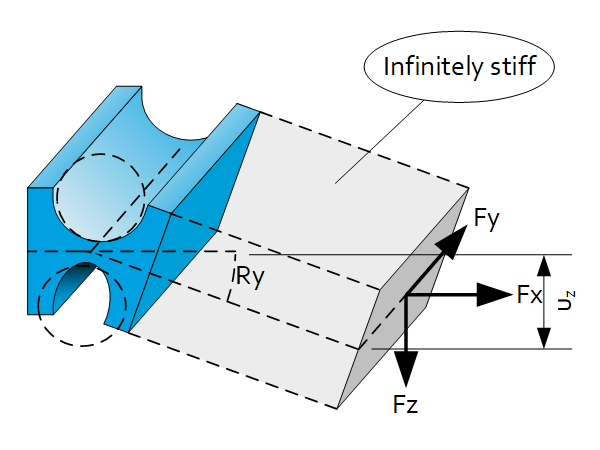
Stiffness at point A $D=frac{2d_1d_2}{d_1+d_2}, D(d_2=infty)=2d_1$ (straight, see below) $C_{Ax}=0.48Etsqrt{frac{h}{D}}$${C_A}_y^ast>frac{GA}{l}=frac{Ght}{D}=frac{Eht}{2D(1+nu)}$ *No acknowledged equation. Above stated equation can only be used as a rough estimate$C_{Az}=0.56Etsqrt{frac{h}{D}}left(frac{1}{1.2+{frac{D}{h}}}right)$ $K_{Ax}=frac{1}{12}t^2cdot C_z=0.047Et^3sqrt{frac{h}{D}}left(frac{1}{1.2+{frac{D}{h}}}right)$ $K_{Ay}=0.093Eth^2sqrt{frac{h}{D}} $$K_{Az}= frac{1}{12}t^2cdot C_x=0.04Et^3sqrt{frac{h}{D}}$ Stiffness at point B $C_{Bx}=C_{Ax} $$frac{1}{C_{By}} =frac{1}{C_{Ay}}+frac{L^2}{K_{Az}} C_{BY}=frac{C_{Ay}K_{Az}}{K_{Az}+C_{Ay}L^2}$$frac{1}{C_{Bz}}=frac{1}{C_{Az}}+frac{L^2}{K_{Ay}} C_{BZ}=frac{C_{Az}K_{Ay}}{K_{Ay}+C_{Az}L^2}$ Other properties $u_z=frac{F_z}{C_{Bz}}$ $R_y=frac{F_zL}{K_{Ay}}$ $sigma_{max}approx0.58Esqrt{frac{h}{D}}R_y=EScdot R_y$ Version with equal $h$, $C_x$ and $K_y$ Design rules of thumb Elastic hinge parameter: […]
Flexure engineering fundamental: Folded leaf spring
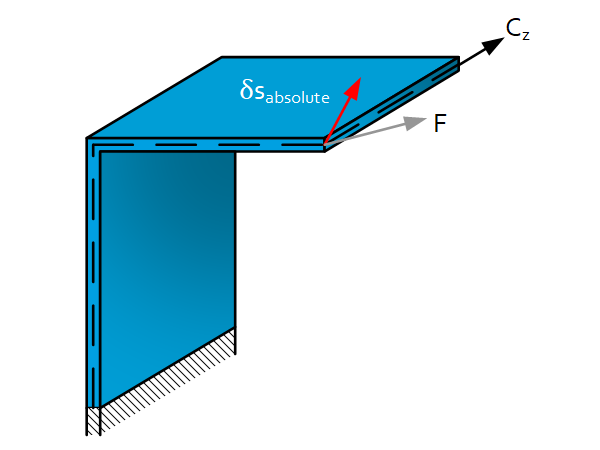
Introduction Folded leaf springs can be used for stiffness in one direction as an alternative for a rod. Pro’s & Con’s No parasitic displacements Force (grey arrow) and displacement (red arrow) are not unidirectional. To obtain an identical direction an additional guiding is necessary and thus ‘extra stiffness’ is introduced. Equations folded leaf spring with […]
Flexure engineering fundamental: Leaf spring
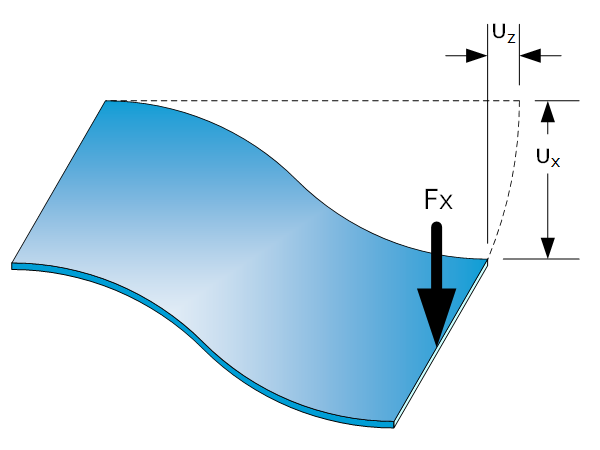
S-shape stiffness $C_x=frac{Ebt^3}{L^3} $$C_y=frac{Etb^3}{L^3} $ if $R_x$ is fixed, $C_y=frac{Etb^3}{4L^3} $ if $R_x$ is free$C_z=frac{EA}{L}$ only if $u_x=0 $$C_z=frac{700EAI_y}{L(700I_y+{u_x}^2A)}$ for $u_xneq0$ $K_x=frac{Etb^3}{12L}$ for $u_x=0$$K_y=frac{Ebt^3}{12L}$ for $u_x=0$$K_z=frac{Gbt^3}{3L}=frac{Ebt^3}{6left(1+nuright)L}$ for $u_x=0$ S-shape motion characteristics $u_x=frac{F_x}{C_x}$$u_{xmax}=frac{1}{3}frac{L^2}{Et}sigma_{max}$$u_z=frac{3}{5}frac{u_x^2}{L}$ S-shape force limits $sigma_{max}=frac{M_{max}}{I}frac{1}{2}t=frac{frac{F_xL}{2}}{I}frac{1}{2}t=frac{F_xLt}{4I}$ dynamic movements: $sigma_{max}<$ fatigue stress limit static deformation: $sigma_{max}<$ yield stress limit $(sigma_{0.2})$ See Beam Theory: Buckling for equations […]
