Third order point-to-point motion profile
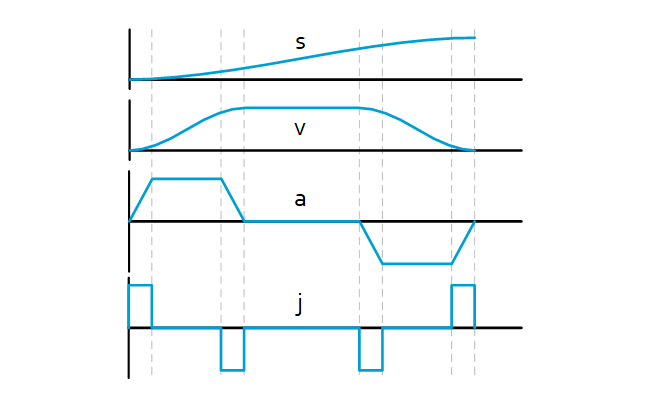
Introduction In many mechatronic applications where a movement from A to B needs to be performed, a third order point to point motion profile is used.To enable early insight in the relevant parameters of a motion profile it is useful to calculate and visualize the relevant parameters (position, speed, acceleration and jerk). This sheet provides […]
Structural damping properties of mechanical systems
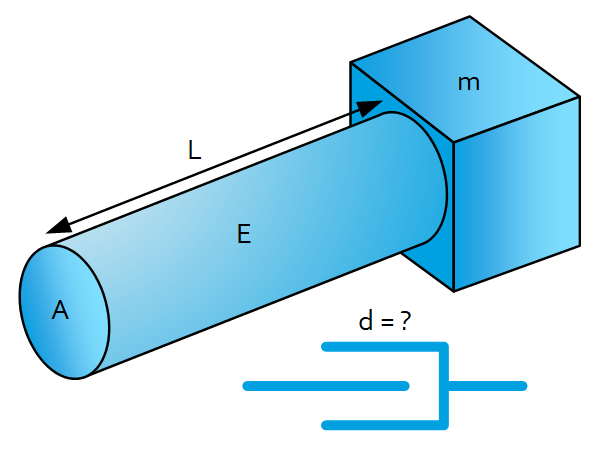
Introduction Each mechanical system from actuator to end-effector comprises damping. This sheet provides some insight how to predict this damping. Damping depends on many factors, such as material, shape, environment, velocity, etc. and therefore it is difficult to predict. Sub- super- and critical damping A critically damped system converges as fast as possible without oscillating […]
Structural damping definitions
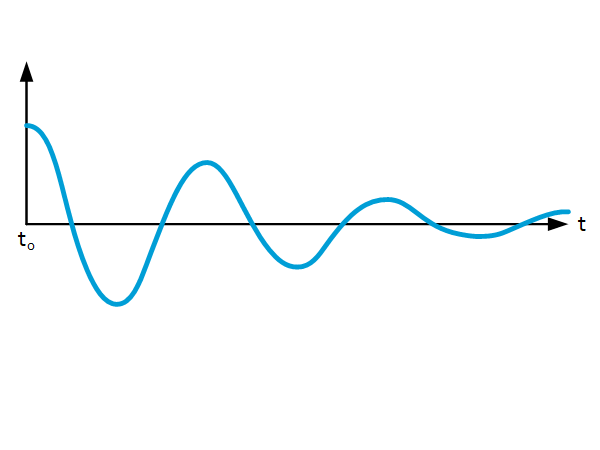
Introduction Every part of a mechanical system, from actuator to end-effector, comprises damping. This sheet gives an overview of ways damping can be defined and how these definitions are related to the linear dimensionless damping coefficient $zeta$. What is damping? Damping in mechanical systems is the extraction of mechanical energy from the motion in the […]
Motion control: Basic feedback design
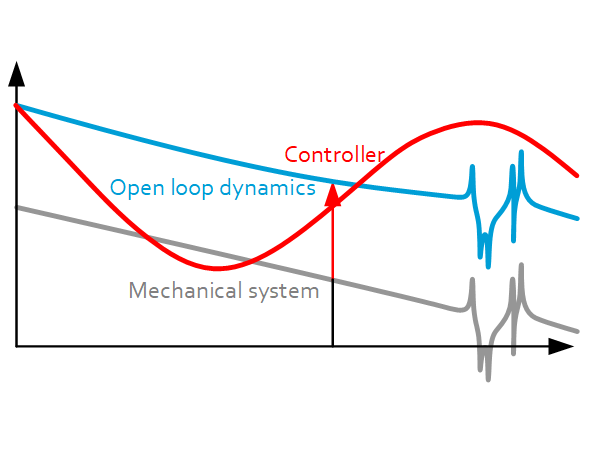
Introduction Motion systems are generally designed to be operated with feedback design control. A common way in industry to design such a controller is carried out by loop shaping, i.e. manually design the open-loop frequency response and interactively evaluate the results on the basis of closed-loop responses (e.g. sensitivity function). Benefits of this approach: It […]
4th order systems: Interpretation
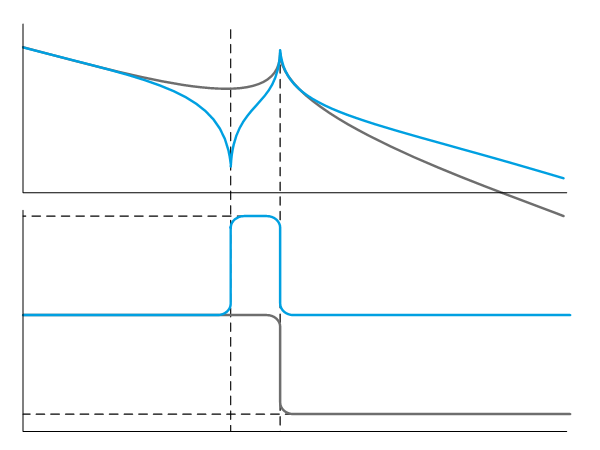
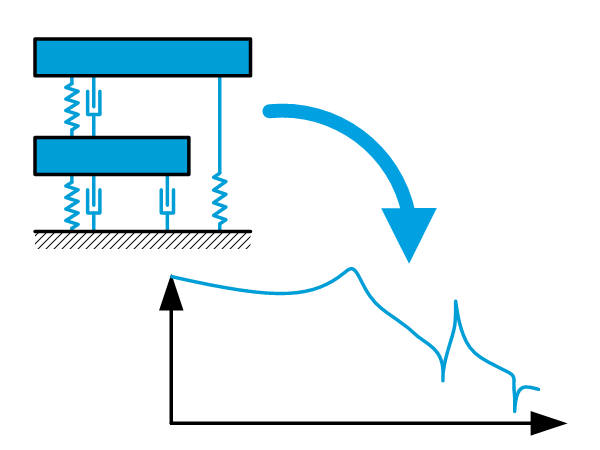
Introduction Due to limited stiffness, a 4th order system or in other words mechanical systems are characterized by internal resonances which limit dynamical performance, both open-loop and closed-loop. To study the impact of this behavior, a simplified model known as the 4th-order system or 2-mass-spring-damper system is often used. This lumped model is often a […]
Dynamic model in state space
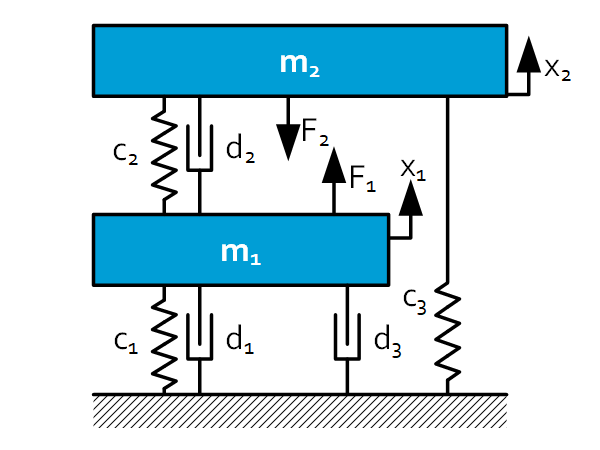
Introduction This sheet is to do a quick scan to the resonances of a desired transfer of a dynamic system via state space approach. From state space a bode-diagram can be created with appropriate software. Equations of Motion (n-dimensional) $underline{M} underline{ddot{x}}+underline{D} underline{dot{x}}+underline{K} underline{x}+underline{F}=underline{0}$ with $underline{x}=left[begin{matrix}x_1&ldots&x_n\end{matrix}right]^Trightarrow n x 1$ $underline{M}=left[begin{matrix}m_1&0&0&0\0&m_2&0&0\0&0&ddots&0\0&0&0&m_n\end{matrix}right]rightarrow n x n$ $underline{K}=left[begin{matrix}K_{11}&K_{12}&ldots&K_{1n}\K_{21}&K_{22}&ldots&K_{2n}\vdots&vdots&ddots&vdots\K_{n1}&K_{n2}&ldots&K_{nn}\end{matrix}right]rightarrow n x n$ […]
Bode plot: Composition and interpretation
Introduction This sheet provides the steps to compose a bode plot of an arbitrary ordinary differential equation. In the resulting bode plot some insights and interpretations are presented, which are also valid for frequency response functions. Composition of bode Step 1: Derive the (Ordinary) Differential Equation$ldots+ mddot{x}+dleft({dot{x}-dot{x}}_{in}right)+cleft(x-x_{in}right)+ldots=F_e$ Step 2: Laplace transform (using $x=x$, $dot{x}=sx$, $ddot{x}=s^2x$, […]
Interpretation of stiffness and damping
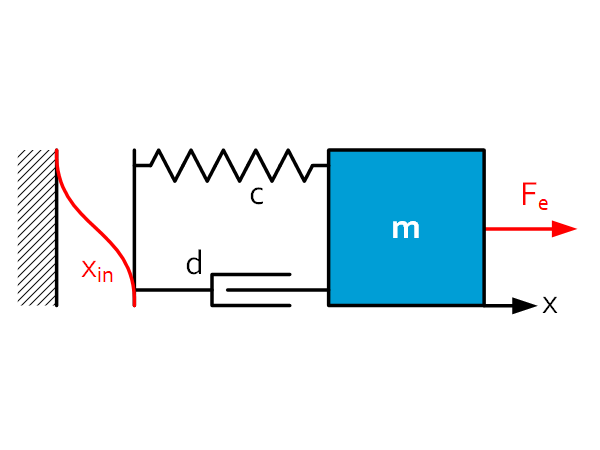
Introduction This sheet gives some insight about stiffness and damping and their effect on the dynamics of mechanical systems. Influence of stiffness Stiffness increases the tracking behavior the displacement x of the end-effector (mass m) in relation to the input $x_{in}$ (a stiff actuator). Moreover, it decreases the influence of the external force $F_e$, which […]
