Buckling fundamentals
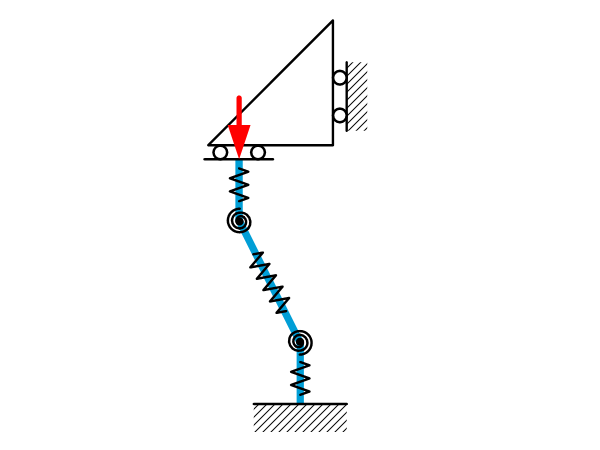
Introduction For slender structures there is a risk that buckling may occur when loaded with compression. This sheet gives an overview of how to interpret buckling and how to identify the potential risks. See Beam theory: Buckling to calculate buckling loads. What is buckling? Buckling is often seen as a failure mode of the material […]
Torsion of leaf springs: Restrained warping
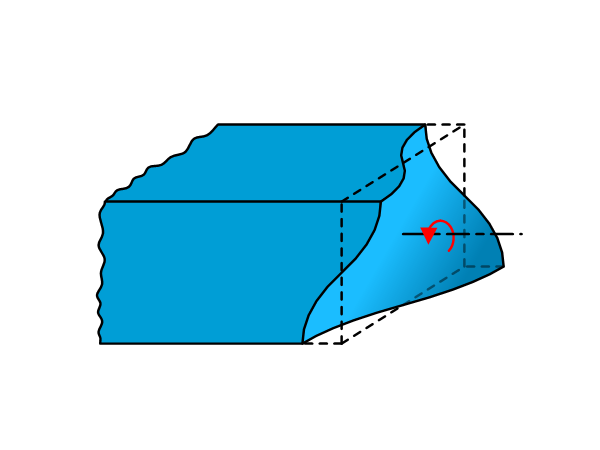
Introduction On page Beam theory: Torsion, the stiffness and shear stress due to applied torsion is presented. These equations assume the cross section of the beam is free to warp, however, this is not always true, specifically in leaf spring design. Warping due to torsion Torsion would cause the cross section of the beam to […]
Beam theory: Buckling
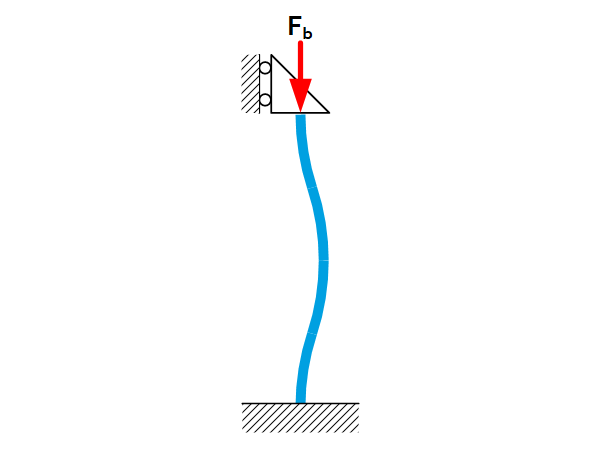
Introduction For slender structures there is a risk that buckling may occur when loaded with compression. This sheet gives the force at which buckling occurs ($F_b$) for beams with various boundary constraints. For more information on buckling see the page Buckling fundamentals. Buckling of uniform beams / leaf springs The buckling force is given by: […]
Beam theory: Stiffness of combined loads

Introduction Most beam theory examples use perfect loading conditions with often a single load. But what happens when the loads are not applied at the perfect location or when a combination of loads is applied? This page aims to give some feel for the change in stiffness by giving two examples; tension/compression combined with bending […]
Vacuum: Rules of thumb
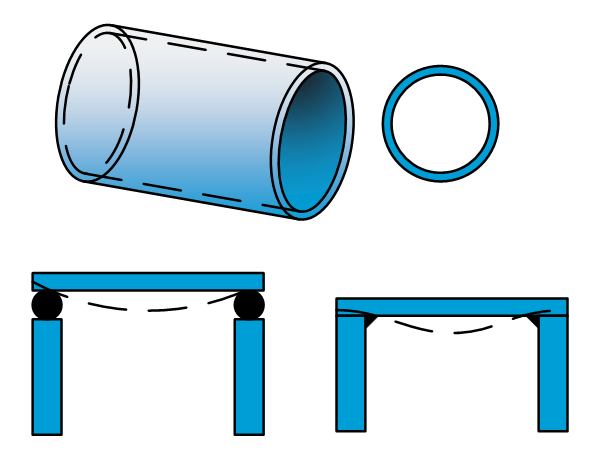
Introduction This sheet will give some basics about a vacuum chamber itself and about mechanical setups that are placed in it. Pressure conversion $1MPa =1frac{N}{mm^2}=145psi=10bar $$1mbar={10}^{-4}MPa=0.0145psi=100frac{N}{m^2}$ Gas law $pV=nRT$ with $R=8.314JK^{-1}mol^{-1}$ Estimates for wall thickness ($p=1$ bar) $tau_{0.2}approx0.4cdotsigma_{0.2}$ (JPE Estimate for metals), $t=$ thickness,$delta=$ deformation Types of leakage Real leakage (holes, porous materials) Virtual leakage […]
Basics on magnetics
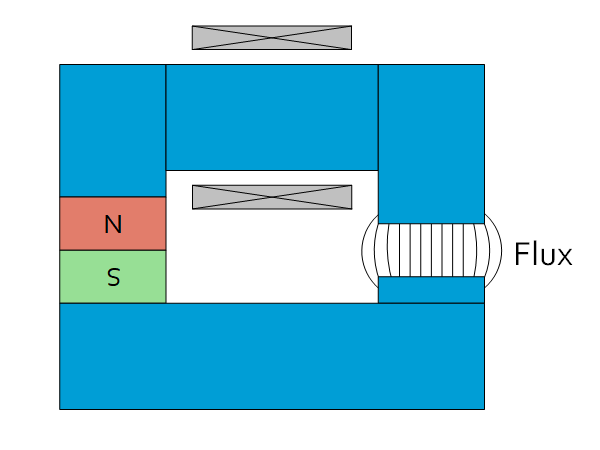
Introduction Magnetism is a physical phenomenon on which many applications rely. It is the basis of not only electric motors and actuators, but also plays an important role in electrical circuits. Magnetic Field The magnetic field $B$ describes the total magnetic field within a material. It is a function of the materials permeability, which is […]
HexaPod: Forces
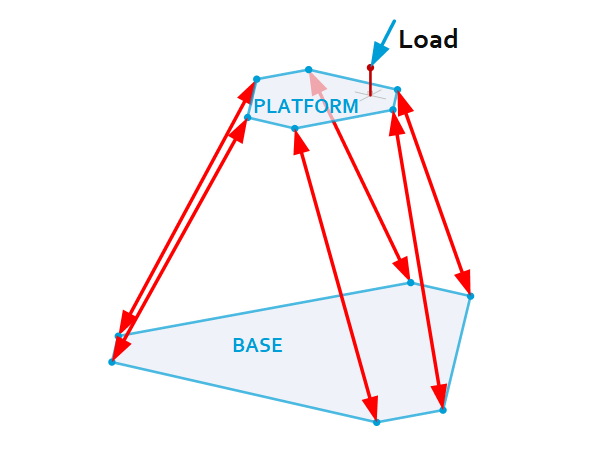
Introduction Hexapod or so-called Stewart platform mechanisms are widely used in precision engineering applications. The big advantage of this mechanism is the parallel linkage of all Degrees Of Freedom (DOF) from the moving platform to the base. In most cases this enables a much stiffer and compact design compared to a conventional mechanism where the […]
HexaPod: Kinematics
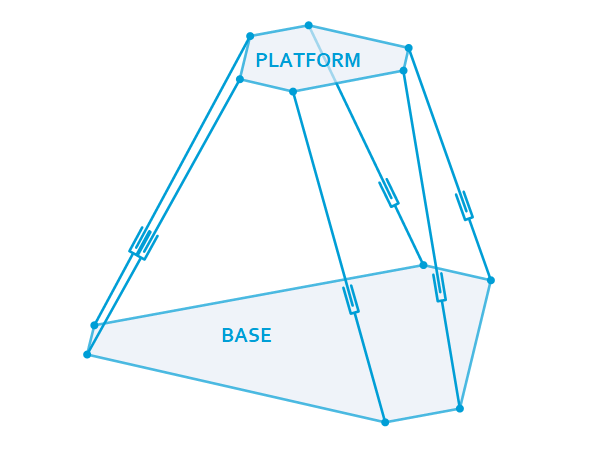
Introduction Hexapod or so-called Stewart platform mechanisms are widely used in precision engineering applications. The big advantage of this mechanism is the parallel linkage of all Degrees Of Freedom (DOF) from the moving platform to the base. In most cases this enables a much stiffer and compact design compared to a conventional mechanism where the […]
Zernike modes & deformable mirrors
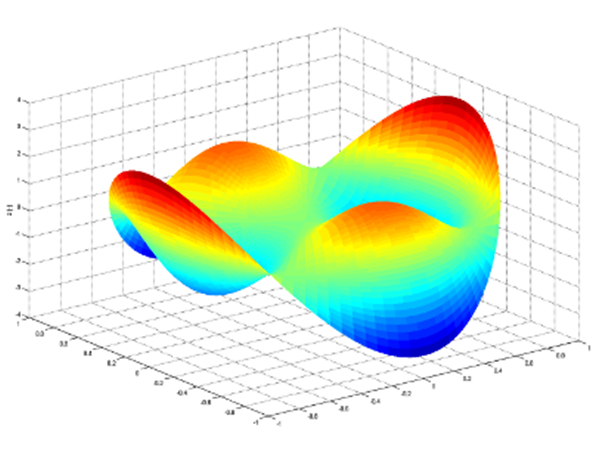
Introduction Zernike modes are an infinite series of polynomials that can be used to describe surface shapes on the unit disk. They are often used in optics to describe and quantify wavefront aberrations in mirrors and lenses with a circular aperture. Definition Zernike polynomials are defined in a polar coordinate system with radius $rho$ and […]
Thin lenses: Practical implementation
Introduction This sheet focuses on the use of spherical lenses in opto-mechanical applications, not on the design of a lens itself. The thin lens equation, chromatic and spherical aberrations, wave lengths and the use of GRIN lenses is discussed. Spherical lenses versus parabolic lenses Spherical lenses have a focal region (see ‘Spherical aberrations’) whereas parabolic […]
