Introduction
Beam theory is such a common engineering fundamental; it is impossible to be omitted from almost any engineering-specialism. However, this sheet incorporates stress and stiffness as well. For more information on, and calculations of the area moment of inertia I, see sheet: Area moment of inertia.
Validity
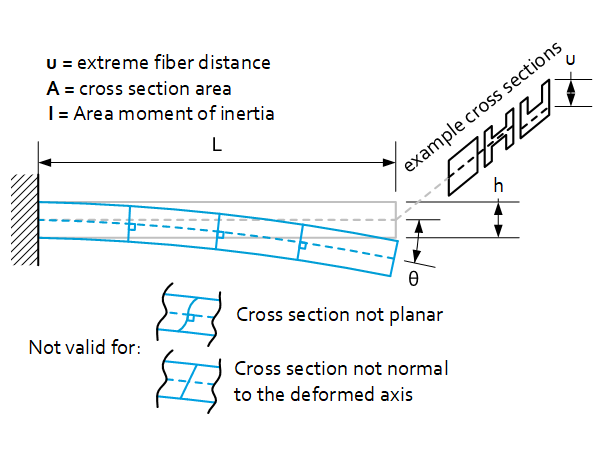
Euler-Bernoulli beam theory is only valid with the following assumptions:
- Cross sections of the beam do not deform in a significant manner under the application of transverse or axial loads and can be assumed as rigid.
- During deformation, the cross section of the beam is assumed to remain planar and normal to the deformed axis of the beam.
Generally, these criteria are met when the beam is a slender beam with small rotations. This means the slenderness of the beam (ratio L/h) should be larger than 10 and the rotation of the neutral axis (θ) should be smaller than 5°.
| Load case | Condition | Curvature $\theta$ Sag $\delta y$ | Reaction force $R$ Shear force $D$ Reaction moment $M_R$ | Stress $\sigma$ Stiffness $C$ |
|---|---|---|---|---|
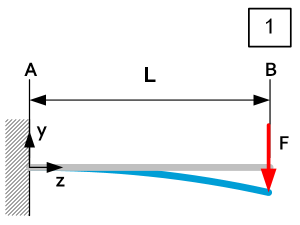 | $\theta_A=0$ $\theta_B=\frac{{\mathrm{FL}}^2}{2EI_x}$ $\delta y_z=-\frac{\left({\rm Fz}^2\right)\left(3L-z\right)}{6EI_x}$ $\delta y_{max}=-\frac{{\rm FL}^3}{3{\rm EI}_x}@\ z=L$ | $R_A=F$ $R_B=N.A.$ $D_z=F$ $M_{Rz}=F\left(z-L\right)$ $M_{Rmax}=-FL\ @\ z=0$ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=-\frac{\left|F\right|u\left(z-L\right)}{I_x}$ $\left|\sigma_{max}\right|=\frac{\left|F\right|Lu}{I_x}@\ z=0$ $\left|C_y\right|=\left|\frac{F}{\delta y_{z\left(F\right)}}\right|=\frac{3{\rm EI}_x}{L^3}\ @\ z=L$ |
|
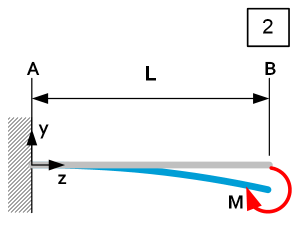 | $\theta_A=0$ $\theta_B=\frac{ML}{{\rm EI}_x}$ $\delta y_z=-\frac{{\rm Mz}^2}{2{\rm EI}_x}$ $\delta y_{max}=-\frac{{\rm ML}^2}{2{\rm EI}_x}@\ z=L$ | $R_A=0$ $R_B=N.A. $ $D_z=N.A. $ $M_{Rz}=M $ $M_{Rmax}=\ M\ @\ z=const. $ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|M\right|u}{I_x}$ $\left|\sigma_{max}\right|=\frac{\left|M\right|u}{I_x}\ \ @\ z=const.$ $\left|K_y\right|=\left|\frac{M}{\theta_B}\right|=\frac{{\rm EI}_x}{L}\ @\ z=L $ |
|
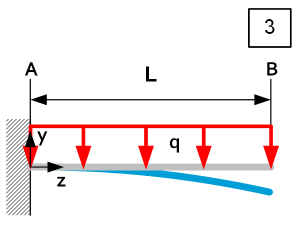 | $\theta_A=0$ $\theta_B=\frac{{\rm qL}^3}{6{\rm EI}_x} $ $\delta y_z=-\frac{{\mathrm{qz}}^2\left(6L^2-4Lz+z^2\right)}{24{\mathrm{EI}}_x}$ $\delta y_{max}=-\frac{{\mathrm{qL}}^4}{8{\mathrm{EI}}_x}@\ z\ =\ L $ | $R_A=qL $ $R_B=N.A. $ $D_z=q\left(L-z\right) $ $M_{Rz}=-\frac{q\left(L-z\right)^2}{2} $ $M_{Rmax}=-\frac{{\rm qL}^2}{2}\ @\ z=0 $ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|q\right|u\left(L-z\right)^2}{2I_x} $ $\left|\sigma_{max}\right|=\frac{\left|q\right|L^2u}{2I_x}@ z=0 $ $\left|C_y\right|=\left|\frac{q}{\delta y_{max}}\right|=\frac{8{\rm EI}_x}{L^4}@\ z=L $ |
|
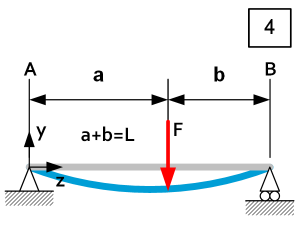 | $0\le z\le a$ | $\theta_A=\frac{Fab\left(L+b\right)}{6{\rm EI}_xL} $ $\theta_B=\frac{Fab\left(L+a\right)}{6{\rm EI}_xL} $ $\delta y_z=-\frac{{\rm Fab}^2}{6{\rm EI}_x}\left[\left(1+\frac{L}{b}\right)\frac{z}{L}-\frac{z^3}{abL}\right] $ $\delta y_{max}=-\frac{Fb\sqrt{\left(L^2-b^2\right)^3}}{9\sqrt3{\rm EI}_xL}\ @\ z=\sqrt{\frac{L^2-b^2}{3}}\ \textsf{only if }a>b$ | $R_A=\ \frac{Fb}{L} $ $R_B=\frac{Fa}{L} $ $D_z=\frac{-Fb}{L} $ $M_{Rz}=\frac{Fbz}{a+b} $ $M_{Rmax}=\frac{Fba}{a+b}\ @\ z=a $ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|F\right|bzu}{I_xL} $ $\left|\sigma_{max}\right|=\frac{\left|F\right|bau}{I_x\left(a+b\right)}\ @\ z=a $ $\left|C_y\right|=\left|\frac{F}{\delta y_{z\left(F\right)}}\right|=\frac{3{\rm EI}_xL}{a^2b^2}\ @\ z=a$ |
| $a\le z\le L$ | $\theta_A=\frac{Fab\left(L+b\right)}{6{\rm EI}_xL} $ $\theta_B=\frac{Fab\left(L+a\right)}{6{\rm EI}_xL} $ $\delta y_z=-\frac{{\rm Fa}^2b}{6{\rm EI}_x}\left[\left(1+\frac{L}{a}\right)\frac{L-z}{L}-\frac{\left(L-z\right)^3}{abL}\right] $ $\delta y_{max}=-\frac{Fa\sqrt{\left(L^2-a^2\right)^3}}{9\sqrt3{\rm EI}_xL}\ @\ z=L-\sqrt{\frac{L^2-a^2}{3}}\ \textsf{only if }b>a$ | $R_A=\frac{Fb}{L} $ $R_B=\frac{Fa}{L}$ $D_z=\frac{Fb}{L}-F $ $M_{Rz}=\left(\frac{Fbz}{L}\right)-F\left(z-a\right) $ $M_{Rmax}=\frac{Fba}{L}\ @\ z=a$ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\ \frac{\left|\left(\frac{Fbz}{L}\right)-F\left(z-a\right)\right|}{I_x}u $ $\left|\sigma_{max}\right|=\frac{\left|F\right|bau}{I_xL}@\ z=a $ $\left|C_y\right|=\left|\frac{F}{\delta y_{z\left(F\right)}}\right|=\frac{3{\rm EI}_xL}{a^2b^2}@\ z=a $ |
|
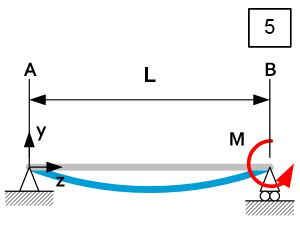 | $\theta_A=\frac{ML}{6{\rm EI}_x} $ $\theta_B=\frac{ML}{3{\rm EI}_x} $ $\delta y_z=-\frac{{\rm ML}^2}{6{\rm EI}_x}\left[\frac{z}{L}-\left(\frac{z}{L}\right)^3\right] $ $\delta y_{max}=-\frac{{\rm ML}^2}{9\sqrt3{\rm EI}_{x\ }}\ @\ z=\frac{L}{\sqrt3} $ | $R_A=\frac{M}{L} $ $R_B=-\frac{M}{L}$ $D_z=\frac{M}{L} $ $M_{Rz}=\left(\frac{M}{L}\right)z $ $M_{Rmax}=M\ @\ z=L $ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|M\right|zu}{{\mathrm{LI}}_x}$ $\left|\sigma_{max}\right|=\frac{\left|M\right|u}{I_x}@\ z=L$ $\left|K_y\right|=\left|\frac{M}{\theta_B}\right|=\frac{3{\mathrm{EI}}_x}{L}\ @\ z=L$ |
|
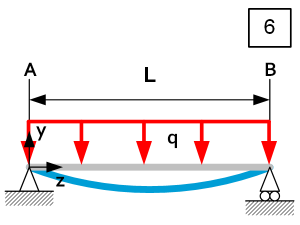 | $\theta_A=\frac{{\rm qL}^3}{24{\rm EI}_x} $ $\theta_B=\frac{{\rm qL}^3}{24{\rm EI}_x} $ $\delta y_z=-\frac{{\rm qL}^4}{24{\rm EI}_x}\left[\frac{z\ }{L}-2\left(\frac{z}{L}\right)^3+\left(\frac{z}{L}\right)^4\ \right] $ $\delta y_{max}=-\frac{5}{384}\frac{{\rm qL}^4}{{\rm EI}_x}\ @\frac{L}{2} $ | $R_A=\frac{qL}{2} $ $R_B=\frac{qL}{2} $ $D_z=\frac{qL}{2}-qz $ $M_{Rz}=\frac{qz\left(L-z\right)}{2} $ $M_{Rmax}=\frac{{\rm qL}^2}{8}\ @\ z=\frac{L}{2} $ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|qz\left(L-z\right)u\right|}{2I_x}$ $\left|\sigma_{max}\right|=\frac{\left|q\right|L^2u}{8I_x}@\ z=\frac{L}{2}$ $\left|C_y\right|=\left|\frac{q}{\delta y_{max}}\right|=\frac{384EI_x}{5L^4}\ @\ z=\frac{L}{2}$ |
|
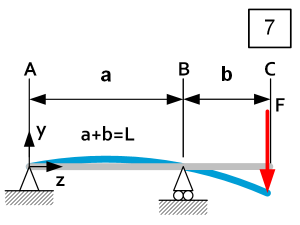 | $0\le z\le a$ | $\theta_A=\frac{FbL}{6{\rm EI}_x}$ $\theta_B=\frac{FbL}{3{\rm EI}_x}$ $\delta y_z=\frac{{\rm Fba}^2}{6{\rm EI}_x}\left[\frac{z}{a}-\left(\frac{z}{a}\right)^3\right]$ $\delta y_{max}=\frac{{\rm Fba}^2}{9\sqrt3{\rm EI}_x}\ @\ z=\frac{a}{\sqrt3}$ | $R_A=-\frac{Fb}{a}$ $R_B=F+\frac{Fb}{a}$ $D_z=-\left(\frac{Fb}{a}\right)$ $M_{Rz}=-\frac{Fbz}{a}$ $M_{Rmax}=-Fb\ @\ z=a$ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|F\right|bzu}{{\rm aI}_x}$ $\left|\sigma_{max}\right|=\frac{\left|F\right|bu}{I_x}@z=a$ $\left|C_y\right|=\left|\frac{F}{\delta y_{z\left(F\right)}}\right|=\frac{3{\rm EI}_x}{b^2L}\ @z=L$ |
| $a\le z\le L$ | $\theta_C=\frac{Fb\left(2a+3b\right)}{3{\rm EI}_x}$ $\delta y_z=\ -\frac{F\left(\left(-z\right)+a\right)}{6{\rm EI}_x}\left[ab-3bz+z^2-2az+a^2\right]$ $\delta y_{max}=-\frac{{\rm Fb}^2L}{3{\rm EI}_x}\ @\ z=L$ | $R_A=-\frac{Fb}{a}$ $R_B=F+\frac{Fb}{a}$ $D_z=F$ $M_{Rz}=-F\left[\left(-z\right)+a+b\right]$ $M_{Rmax}=-Fb\ @\ z=a$ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|F\right|\left[\left(-z\right)+L\right)}{I_x}u$ $\left|\sigma_{max}\right|=\frac{\left|F\right|bu}{I_x}\ @z=a$ $\left|C_y\right|=\left|\frac{F}{\delta y_{z\left(F\right)}}\right|=\frac{3{\rm EI}_x}{b^2L}\ @z=L$ |
|
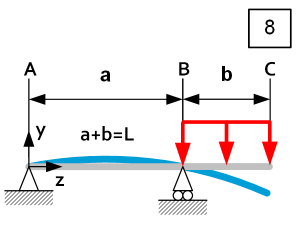 | $0\le z\le a$ | $\theta_A=\frac{{\rm qb}^2a}{12{\rm EI}_x} $ $\theta_B=\frac{{\rm qb}^2a}{6{\rm EI}_x} $ $\delta y_z=\frac{{{\rm qb}^2a}^2}{12{\rm EI}_x}\left[\frac{z}{a}-\left(\frac{z}{a}\right)^3\right] $ $\delta y_{max}=\frac{{{\rm qb}^2a}^2}{18\sqrt3{\rm EI}_x}\ @\ z=\frac{a}{\sqrt3}$ | $R_A=-\frac{{\rm qb}^2}{2a} $ $R_B=\frac{qb\left(b+2a\right)}{2a} $ $D_z=-\frac{{\rm qb}^2}{2a} $ $M_{Rz}=-\left(\frac{{\rm qb}^2}{2a}\right)z $ $M_{Rmax}=-\frac{{\rm qb}^2}{2}\ \ @\ z=a $ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|q\right|b^2zu}{2{\rm aI}_x} $ $\left|\sigma_{max}\right|=\frac{\left|q\right|b^2u}{2I_x}\ \ @\ z=a $ $\left|C_y\right|=\left|\frac{q}{\delta y_{max}}\right|=\frac{18\sqrt3{\mathrm{EI}}_x}{b^2a^2}\ @\ z=\frac{a}{\sqrt3} $ |
| $a\le z\le L$ | $\theta_C=\frac{{\rm qb}^2L}{6{\rm EI}_x} $ $\delta y_z=\ -\frac{{\rm qb}^4}{24{\rm EI}_x}\left[4\frac{a}{b}\frac{z-a}{b}+6\left(\frac{z-a}{b}\right)^2-4\left(\frac{z-a}{b}\right)^3+{\left(\frac{z-a}{b}\right)}^4\right]$ $\delta y_{max}=-\frac{{\rm qb}^3\left(4a+3b\right)}{24{\rm EI}_x}\ @\ \mathrm{z}=L $ | $R_A=\ -\frac{{\rm qb}^2}{2a} $ $R_B=\frac{qb\left(b+2a\right)}{2a} $ $D_z=qb-q\mathrm{(z+a)} $ $M_{Rz}=\frac{-q\left(b^2-2bz+{\mathrm{2ba+z}}^2-2za+a^2\right)}{2} $ $M_{Rmax}=-\frac{{\rm qb}^2}{2}\ \ @\ z=a $ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u= \frac{\left|qu\left(b^2-{2bz+{\mathrm{2ba+z}}^2-2za+a}^2\right)\right|}{2I_x} $ $\left|\sigma_{max}\right|=\frac{\left|q\right|b^2u}{2I_x}\ \ @\ z=a $ $\left|C_y\right|=\left|\frac{q}{\delta y_{max}}\right|=\frac{24{\rm EI}_x}{b^3\left(4a+3b\right)}\ @\ \mathrm{z}=L $ |
|
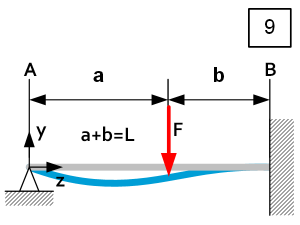 | $0\le z\le a$ | $\theta_A=\frac{{\rm Fab}^2}{4{\rm EI}_xL} $ $\theta_B=0 $ $\delta y_z=-\frac{{\rm FLb}^2}{4{\rm EI}_x}\left[\frac{az}{L^2}-\frac{2}{3}\left(1+\frac{a}{2L}\right)\left(\frac{z}{L}\right)^3\right] $ $\delta y_{max}=-\frac{{\rm ab}^2F\sqrt{\frac{a}{2L+a}}}{6{\rm EI}_x}@z=L\cdot\sqrt{\frac{\frac{a}{2L}}{1+\frac{a}{2L}}}$ $\textsf{Only if }a \geq 0.414L$ | $R_A=F\left(\frac{b}{L}\right)^2\left(1+\frac{a}{2L}\right) $ $R_B=F\left(\frac{a}{L}\right)^2\left(1+\frac{b}{2L}+\frac{3}{2}\frac{b}{a}\right) $ $D_z=F\left(\frac{b}{L}\right)^2\left(1+\frac{a}{2L}\right) $ $M_{Rz}=\ Fz\left(\frac{b}{L}\right)^2\left(1+\frac{a}{2L}\right)$ $M_{Rmax}=\frac{{\mathrm{Fab}}^2}{L^2}\left(1+\frac{a}{2L}\right)$ $@\ z=a\textsf{, with}\ a\le0.414L $ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|F\right|{\rm zb}^2u\left(2L+a\right)}{2L^3I_x} $ $\left|\sigma_{max}\right|=\frac{\left|F\right|{\rm ab}^2u\left(1+\frac{a}{2L}\right)}{L^2I_x}$ $@\ z=a, \textsf{with }a\le 0.414L$ $\left|C_y\right|=\left|\frac{F}{\delta y_{z\left(F\right)}}\right|=\left|\frac{12{\rm EI}_xL^3}{b^2a^2\left[3L^2-2aL-a^2\right]}\right|\ @\ z=a $ |
| $a\le z\le L$ | $\theta_A=\frac{{\rm Fab}^2}{4{\rm EI}_xL} $ $\theta_B=0 $ $\delta y_z=\frac{Fa\left(L-z\right)^2}{12L^3}\frac{2{\rm La}^2-3L^2z+a^2z}{{\rm EI}_x} $ $\delta y_{max}=\delta\ y_z\left(z_{max}\right)\ @\ z_{max}=L\cdot\left[\frac{2aL+bL-ba}{2aL+3bL+ba}\right]$ $\textsf{Only if }a \le 0.414L$ | $R_A=\ F\left(\frac{b}{L}\right)^2\left(1+\frac{a}{2L}\right)$ $R_B=F\left(\frac{a}{L}\right)^2\left(1+\frac{b}{2L}+\frac{3}{2}\frac{b}{a}\right) $ $D_z=-F\left(\frac{a}{L}\right)^2\left(1+\frac{b}{2L}+\frac{3}{2}\frac{b}{a}\right) $ $M_{Rz}=\ Fz\left(\frac{b}{L}\right)^2\left(1+\frac{a}{2L}\right)-F\left(z-a\right) $ $M_{Rmax}=-F\frac{ab}{L}\left(1-\frac{b}{2L}\right)$ $@\ z=L\textsf{, with}\ a\geq0.414L $ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|Fu\left(2{\rm zLb}^2+b^2za-2L^3z+2L^3a\right)\right|}{2L^3I_x}$ $\left|\sigma_{max}\right|=\frac{\left|Fabu\left(1-\frac{b}{2L}\right)\right|}{{\rm LI}_x}$ $@\ z=L\textsf{, with}\ a\geq0.414L $ $\left|C_y\right|=\left|\frac{F}{\delta y_{z\left(F\right)}}\right|=\left|\frac{12{\rm EI}_xL^3}{b^2a^2\left[3L^2-2aL-a^2\right]}\right|\ @\ z=a $ |
|
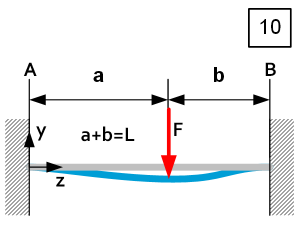 | $0\le z\le a$ $b>a$ | $\theta_A=0 $ $\theta_B=0 $ $\delta y_z=-\frac{{\rm FLa}^2}{6{\rm EI}_x}\left[3\frac{b}{L^3}\left(L-z\right)^2-\left(1+\frac{2b}{L}\right)\frac{\left(L-z\right)^3}{L^3}\right] $ $\delta y_{max}=-\frac{2}{3}\frac{{\rm Fa}^3b^2}{{\rm EI}_xL^2}\left(\frac{1}{1+\frac{2a}{L}}\right)^2\ @\ z=L\frac{1}{1+\frac{L}{2a}}$ | $R_A=F\left(\frac{b}{L}\right)^2\left(1+\frac{2a}{L}\right) $ $R_B=F\left(\frac{a}{L}\right)^2\left(1+\frac{2b}{L}\right) $ $D_z=F\left(\frac{b}{L}\right)^2\left(1+\frac{2a}{L}\right)$ $M_{Rz}=\frac{{\rm Fb}^2\left(zL+2za+aL\right)}{L^3} $ $M_{Rmax}=-\frac{{\rm Fab}^2}{L^2}\ @\ z=0 $ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|Fu\left[b^2zL+2b^2za+b^2aL-L^3z+L^3a\right]\right|}{L^3I_x} $ $\left|\sigma_{max}\right|=\frac{\left|F\right|{\rm uba}^2}{L^2I_x}@\ z=L $ $\left|C_y\right|=\left|\frac{F}{\delta y_{z\left(F\right)}}\right|=\frac{3{\rm EI}_xL^3}{b^2a^3\left(L-a\right)} @\ z=a$ |
| $a\le z\le L$ $a>b$ | $\theta_A=0 $ $\theta_B=0 $ $\delta y_z=-\frac{{\mathrm{FLa}}^2}{6{\mathrm{EI}}_x}\left[3\frac{b}{L^3}\left(L-z\right)^2- \left(1+\frac{2b}{L}\right)\frac{\left(L-z\right)^3}{L^3}\right] $ $\delta y_{max}=-\frac{2}{3}\frac{{\mathrm{Fa}}^3b^2}{{\mathrm{EI}}_xL^2}\left(\frac{1}{1+\frac{2a}{L}}\right)^2@\ z=L\frac{1}{1+\frac{L}{2a}} $ | $R_A=F\left(\frac{b}{L}\right)^2\left(1+\frac{2a}{L}\right) $ $R_B=F\left(\frac{a}{L}\right)^2\left(1+\frac{2b}{L}\right) $ $D_z=-F\left(\frac{a}{L}\right)^2\left(1+\frac{2b}{L}\right) $ $M_{Rz}=\frac{F\left[b^2zL+2b^2za+b^2aL-L^3z+L^3a\right]}{L^3} $ $M_{Rmax}=-\frac{{\rm Fba}^2}{L^2}@\ z=L$ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|Fu\left[b^2zL+2b^2za+b^2aL-L^3z+L^3a\right]\right|}{L^3I_x} $ $\left|\sigma_{max}\right|=\frac{\left|F\right|{\mathrm{uba}}^2}{L^2I_x}\ @\ z=L $ $\left|C_y\right|=\left|\frac{F}{\delta y_{z\left(F\right)}}\right|=\frac{3{\mathrm{EI}}_xL^3}{b^2a^3\left(L-a\right)}\ @\ z=a $ |
|
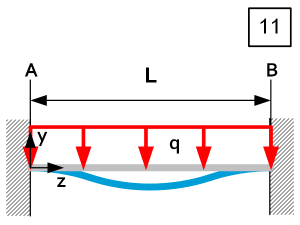 | $\theta_A=0$ $\theta_B=0 $ $\delta y_z=-\frac{{\rm qL}^4}{24{\rm EI}_x}\left[\left(\frac{z}{L}\right)^2-2\left(\frac{z}{L}\right)^3+\left(\frac{z}{L}\right)^4\right] $ $\delta y_{max}=-\frac{{\rm qL}^4}{384{\rm EI}_x}\ @\ z=\frac{L}{2} $ | $R_A=\frac{1}{2}qL$ $R_B=\frac{1}{2}qL $ $D_z=\frac{qL}{2}-qz $ $M_{Rz}=\frac{q\left({-6z}^2+6Lz-L^2\right)}{12} $ $M_{Rmax}=-\frac{{\rm qL}^2}{12}\ @\ \frac{z=0}{z=L} $ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|uq\left({-6z}^2+6Lz-L^2\right)\right|}{12I_x} $ $\left|\sigma_{max}\right|=\frac{\left|q\right|L^2u}{12I_x}\ @\ \frac{z=0}{z=L} $ $\left|C_y\right|=\left|\frac{q}{\delta y_{max}}\right|=\frac{384{\rm EI}_x}{L^4}\ @\ \mathrm{z}=\frac{L}{2} $ |
|
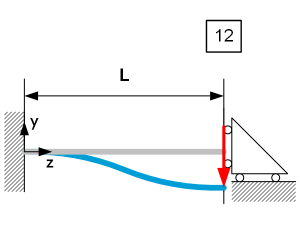 | $\theta_A=0$ $\theta_B=0 $ $\delta y_z=-\frac{{\rm Fz}^2\left(3L-2z\right)}{12{\rm EI}_x} $ $\delta y_{max}=-\frac{{\rm FL}^3}{12{\rm EI}_x}\ @\ z=L $ | $R_A=F $ $R_B=0 $ $D_z=F $ $M_{Rz}=\frac{FL-2Fz}{2} $ $M_{Rmax}=\frac{FL}{2}\ resp.\ -\frac{FL}{2}$ $@\ z=0\ resp.\ L $ | $\left|\sigma_z\right|=\frac{\left|M_{Rz}\right|}{I_x}u=\frac{\left|u\left(FL-2Fz\right)\right|}{2I_x} $ $\left|\sigma_{max}\right|=\frac{\left|F\right|Lu}{2I_x}\ @\ \frac{z=0}{z=L} $ $\left|C_y\right|=\left|\frac{F}{\delta y_{max}}\right|=\frac{12{\rm EI}_x}{L^3}\ @\ z=L $ |
