Introduction
2 leaf springs in parallel are often use as a (quasi-) linear guidance were play must be eliminated.
Pro’s & con’s
- Play/backlash free
- Well predictable stiffness ($C_x$)
- (small) Stiffness in direction of movement
- Parasitic displacements ($u_z$)
- Short stroke
Elimination of parasitic displacements
Through a double parallel leaf spring (in series) the parasitic displacement can be eliminated, like:
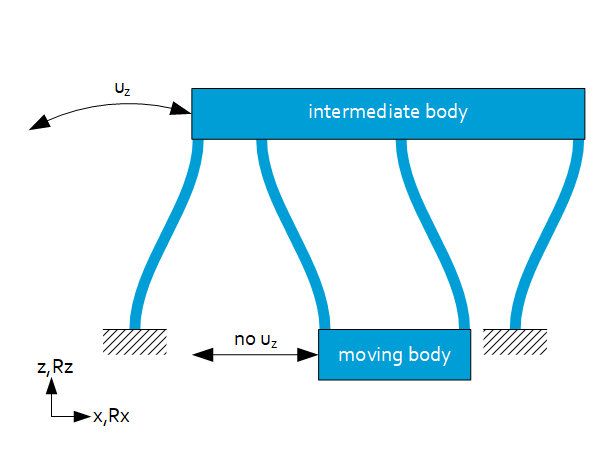
The drive stiffness ($C_x$) halves; however the guiding stiffness ($C_z$) halves as well.
Leaf spring configuration
For machinability, often reinforced leaf springs or 2 elastic hinges in series are used as an alternative per leaf spring. If so use the following guide-lines:
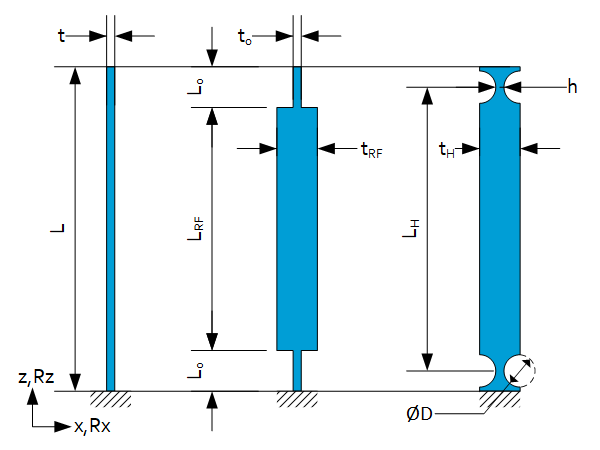
Leaf spring with L,b,t then:
$L_0=\frac{1}{6}L$
$t_0=0.9t$
$t_{RF}=5t_0$
$L_H=\frac{5}{6}L$
$h=\frac{1}{2}t$
$D=2h$
(matching movement)
(matching $C_x$)
(guideline for reinforcement)
(matching movement)
(elastic hinge guide line)
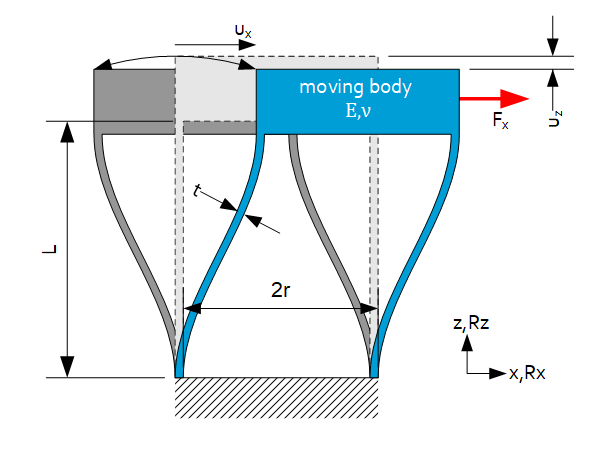
Stiffness
$C_x=2\frac{12EI_z}{L^3}=\frac{2Ebt^3}{L^3} $
$C_y=2\frac{3EI_x}{L^3}=\frac{Eb^3t}{2L^3} $
$C_z=2\frac{EA}{L}=\frac{2Ebt}{L}$ only if $u_x=0$
$C_z=\frac{2}{\frac{L}{EA}+\frac{u_x^2L}{700EI_y}}=\frac{350Ebt^3}{\left(175t^2+3u_x^2\right)L}$ for $u_x\neq0$
$K_x=2\frac{EI_x}{L}=\frac{Eb^3t}{6L} $
$K_y=C_zr^2=\frac{2Ebtr^2}{L} $
$K_z=C_yr^2=\frac{Eb^3tr^2}{2L^3}$
Motion
$u_x=\frac{L^2\sigma}{3Et}$ , $u_z=\frac{3}{5}\frac{u_x^2}{L}\ $
dynamic movements: $\sigma_{max}<$ fatigue stress limit
static deformation: $\sigma_{max}<$ yield stress limit ($\sigma_{0.2}$)
Overconstrained design
Essentially, 2 parallel leaf springs are over constrained. This could be overcome if internal elasticity is introduced like low torsion stiffness of the moving body or notching 1 out of 2 leaf springs. Practically, the best way is to machine the fixed world, the leaf spring and the moving body monolithically.
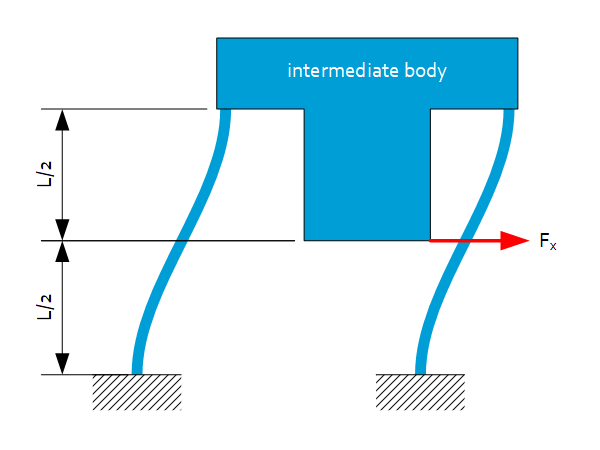
Applying Force Fx
To ensure identical normal force on each leaf spring and thus; a pure linear guidance, the force $F_x$ should be applied at $L/2$ as depicted below.