Introduction
The area moment of inertia (also referred to as second moment of area) is a geometrical property of a shape describing the distribution of points around an axis. In classical mechanics it is used as a measure of a body’s resistance against bending.
Note that next to the area moment of inertia, the polar moment of inertia is used as a measure of a body’s resistance to torsion (see Beam theory: Torsion sheet). Also, the area moment of inertia should not be confused with the mass moment of inertia, which is used as a measure of how an object resists rotational acceleration about a particular axis (see Mass moment of inertia sheet). The area moment of inertia is typically denoted with an I and has an axis that lies in the plane, the polar second moment of inertia is typically denoted with a J and has an axis perpendicular to the plane.
| Cross-section | Area moment of inertia |
|---|---|
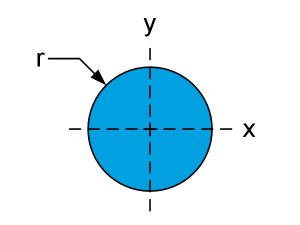 | $$I_x=I_y=\frac{\pi}{4}r^4$$ |
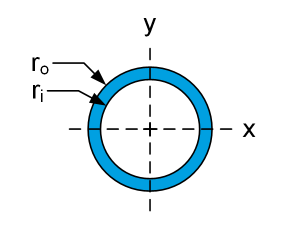 | $$I_x=I_y=\frac{\pi}{4}\left(r_o^4-r_i^4\right)$$ |
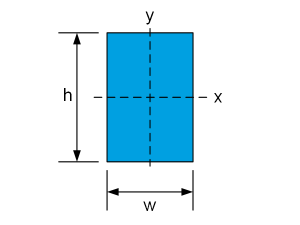 | $$I_x=\frac{{wh}^3}{12}$$ $$I_y=\frac{w^3h}{12}$$ |
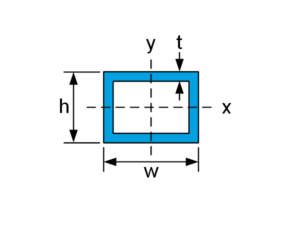 | $$I_x=\frac{w_oh_o^3-w_ih_i^3}{12}$$ $$I_y=\frac{w_o^3h_o-w_i^3h_i}{12}$$ |
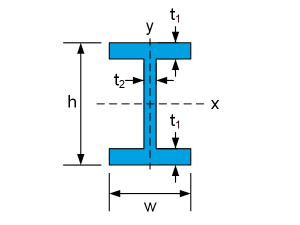 | $$I_x=\frac{wh^3}{12}-\frac{\left(w-t_2\right)\left(h-2t_1\right)^3}{12}$$ $$I_y=\frac{t_2^3\left(h-2t_1\right)}{12}+\frac{2w^3t_1}{12}$$ |
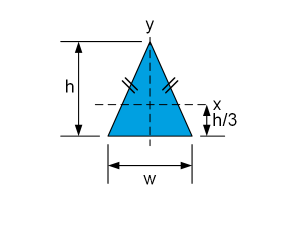 | $$I_x=\ \frac{wh^3}{36}$$ $$I_y=\frac{w^3h}{48}$$ |
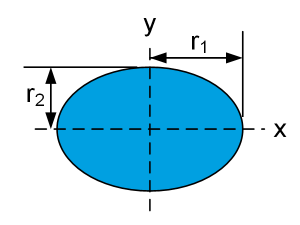 | $$I_x=\frac{\pi}{4}{r_1r}_2^3$$ $$I_y=\frac{\pi}{4}r_1^3r_2$$ |
