Introduction
Most beam theory examples use perfect loading conditions with often a single load. But what happens when the loads are not applied at the perfect location or when a combination of loads is applied? This page aims to give some feel for the change in stiffness by giving two examples; tension/compression combined with bending due to off-center loading and shear combined with bending.
Off-center Tension/Compression
General energy equation
$U=\frac{C\cdot\Delta l^2}{2}=\frac{C\cdot\left(\frac{F}{C}\right)^2}{2}=\frac{F^2}{2C}$
Tensile load energy
$C_t=\frac{E\cdot w\cdot h}{l}$
$U_t=\frac{F_z^2}{2C_t}=\frac{F_z^2l}{2E\cdot w\cdot h}$
Bending load energy
$\theta=\frac{M\cdot l}{E\cdot I_x}=\frac{12F_z\cdot u\cdot l}{E\cdot w\cdot h^3\ } $
$\delta_z=\theta\cdot u $
$C_b=\frac{F_z}{\delta_z}=\frac{E\cdot w\cdot h^3}{12\cdot u^2\cdot l} $
$U_b=\frac{F_z^2}{2C_b}=\frac{6F_z^2\cdot u^2\cdot l}{E\cdot w\cdot h^3}$
Combined load energy
$U_c=U_t+U_b=\frac{F_z^2}{2}\left(\frac{l}{E\cdot w\cdot h}+\frac{12u^2\cdot l}{E\cdot w\cdot h^3}\right)$
$C_c=\frac{E\cdot w\cdot h}{l\left(1+12\left(\frac{u}{h}\right)^2\right)}$
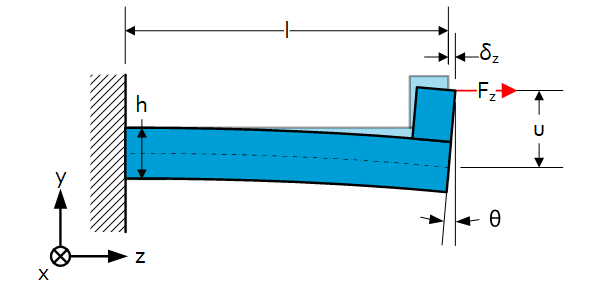
Stiffness of combined load in comparison with tensile load
$\frac{C_c}{C_t}=\frac{\frac{E\cdot w\cdot h}{l\left(1+12\left(\frac{u}{h}\right)^2\right)}}{\frac{E\cdot w\cdot h}{l}}=\frac{1}{1+12\left(\frac{u}{h}\right)^2} $
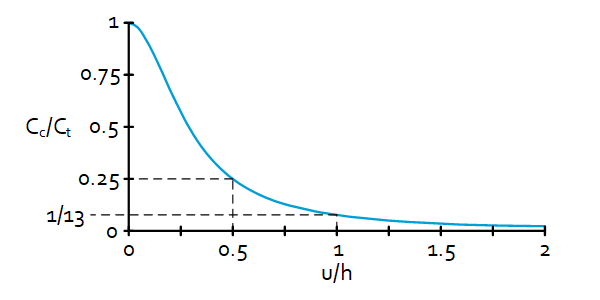
Note: when a load is applied to the outer fiber of the beam ($u=0.5h$) the stiffness $C_c$ of the beam will be 4 times as low as when the beam is loaded at its centerline:
$C_c=\frac{1}{4}\cdot\frac{E\cdot w\cdot h}{l}$
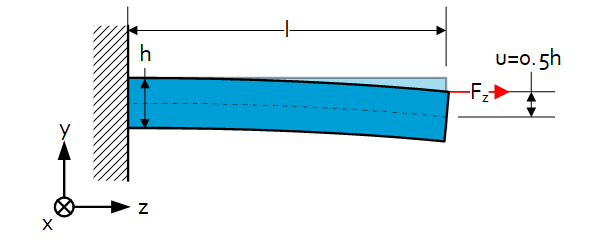
Shear and Bending
Bending stiffness
$C_b=\frac{3EI_y}{l^3}=\frac{Ewh^3}{4l^3}$
Shear stiffness
$C_s=\frac{F_y}{\delta_y}=\frac{G\cdot A}{l}=\frac{\frac{Ewh}{2\left(1+\nu\right)}}{l}=\frac{0.385E\cdot w h}{l} $
Note: this assumes the shear stress has a uniform distribution over the cross section of the beam. Also at the location where the force is introduced!
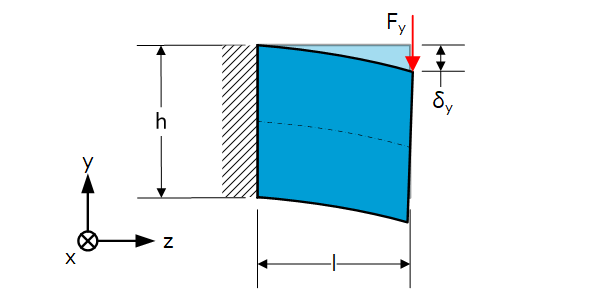
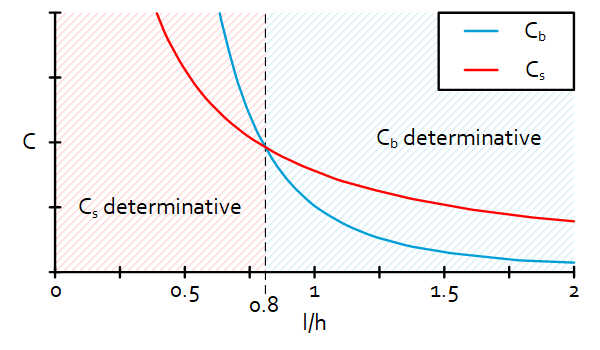
Determinative stiffness depending on beam dimensions
In the figure shown below the bending stiffness $C_b$ and the shear stiffness $C_s$ are illustrated as a function of the ratio $\frac{l}{h}$ between the length $l$ and the height $h$ of the beam. When $\frac{l}{h}\approx0.8$ the bending and shear stiffness are equal. When $\frac{l}{h}<0.8$ the lower value of the shear stiffness is determinative, when $\frac{l}{h}>0.8$ the lower value of the bending stiffness is determinative.