Introduction
When a straight beam is subjected to an axial moment, each cross-section twists around its torsional center. Shear stresses occur within the cross-sectional planes of the beam.
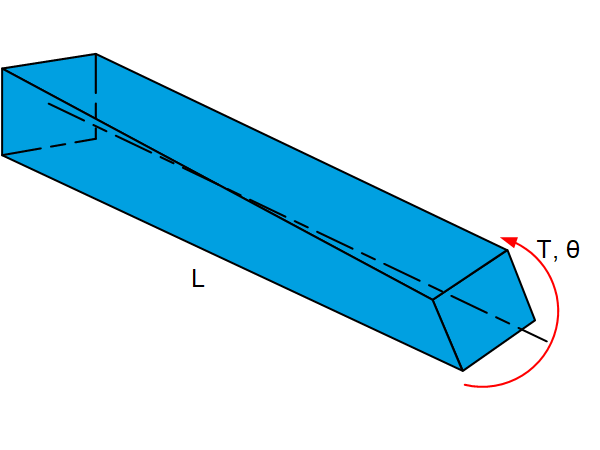
Angular twist
For a torsionally loaded beam, the angular twist is described by:
$$\theta=\frac{T\cdot L}{G\cdot J_T}$$
$J_T$ is the torsion constant. It is equal to the polar moment of inertia $I_z$ if the cross section is circular. For non-circular cross sections warping occurs which reduces the effective torsion constant. For these shapes, approximate solutions of the torsion constant and maximum stress are given in the table below. When no warping can occur see the equations on page Torsion of leaf springs: Restrained warping.
$G$ is the shear modulus. The relation between the shear modulus $G$ and the elastic modulus $E$ is defined by the following formula:
$$G=\frac E{2\left(1+v\right)}\approx 0.38E \textsf{ (For most metals)}$$
Rotational stiffness
The rotational stiffness of a torsionally loaded beam is:
$$K_z=\frac{T}{\theta}=\frac{G\cdot J_T}{L}$$
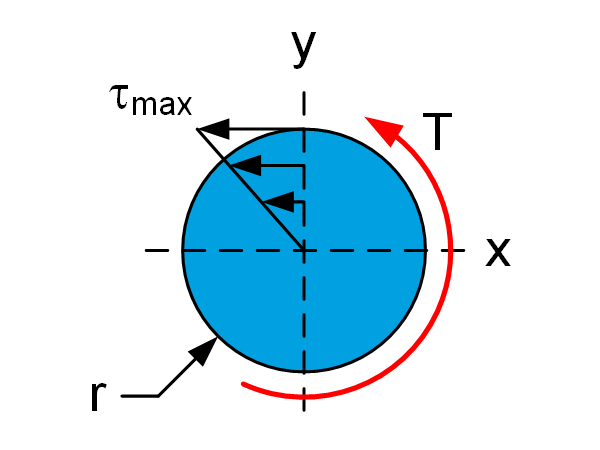
Maximum shear stress
For a torsionally loaded beam with a circular cross-section, the maximum shear stress can be calculated with:
$$\tau_{max}=\frac{Tr}{J_T}$$
For non-circular cross-sections the equations in the table below can be used.
For pure shear, the Von Mises stress is then equal to:
$$\sigma_V=\sqrt3\tau_{max}$$
| Cross section | Condition | Torsion constant $J_T$ | Maximum shear stress $\tau_{max}$ |
|---|---|---|---|
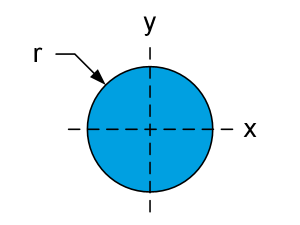 | $$J_T=I_Z=\frac{\pi}{2}r^4$$ | $$\tau_{max}=\frac{2T_{max}}{{\pi}r^3}$$ | |
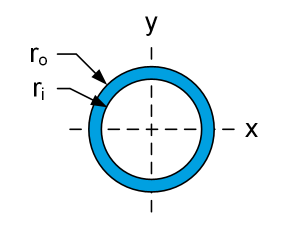 | $$J_T=I_Z=\frac{\pi}{2}(r_o^4-r_i^4)$$ | $$\tau_{max}=\frac{2T_{max}r_o}{\pi\left(r_o^4-r_i^4\right)}$$ | |
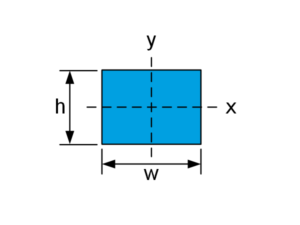 | $$h=w$$ | $$J_T=\frac{9}{64}w^4$$ | $$\tau_{max}=\frac{4.808T}{w^3}$$ |
| $$w\geq\ h$$ | $$J_T=\frac{1}{16}wh^3\left(\frac{16}{3}-3.36\frac{h}{w}\left(1-\frac{h^4}{12w^4}\right)\right)$$ $$\approx\frac{1}{3}wh^3\textsf{ for } w\gg h$$ | $$\tau_{max}=\frac{3T}{wh^2}\left(1+0.6095\frac{h}{w}+0.8865\left(\frac{h}{w}\right)^2-1.8023\left(\frac{h}{w}\right)^3+0.9100\left(\frac{h}{w}\right)^4\right)$$ $$\approx\frac{3T}{wh^2}\textsf{ for } w\gg\ h$$ |
|
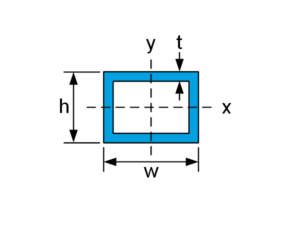 | For thin walled structures | $$J_t=\frac{2t^2\left(w-t\right)^2\left(h-t\right)^2}{\left(w+h\right)t-2t^2}$$ | $$\tau_{average}=\frac{T}{2t(w-t)(h-t)}$$ Note: stress is nearly uniform if t is small. There will be higher stresses at inner corners unless fillets of fairly large radius are provided. |
