Introduction
Cross spring pivots are an interesting alternative for common flexure pivots in case transverse loads of the pivot are relatively high. The layout of a cross spring pivot can be chosen to optimize for large angular motion, or for optimal pivot behavior which is unbiased with parasitic displacements.
Stiffness
To get an idea of the rotational stiffness of a cross spring pivot we first take a look at a reference situation in which the leaf springs don’t cross but have a virtual pivot above.
For two leaf springs that both have the same width $w$ and thickness $t$, and for which its pole is located at a distance $a\cdot L$ along the leaf springs the rotational stiffness is given by:
$K_{z}=8\left(1-3a+3a^2\right)\frac{EI}{L}=8\left(1-3a+3a^2\right)\frac{Ewt^3}{12L}$
With $I$ the area moment of inertia of a single leaf spring.
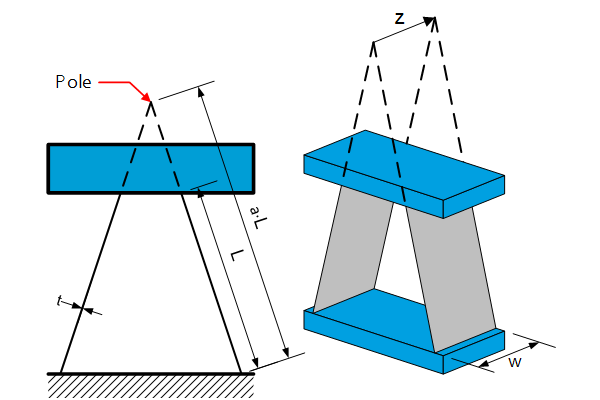
This equation also applies to cross spring pivots in which $a<1$, and where the pole will lie within the mechanism (see examples below).
Reference equations
Rotational stiffness (for $a=0.5$):
$K_{ref}=2\frac{EI}{L}=\frac{Ewt^3}{6L}$
Buckle load (radial):
${F_b}_{ref}=8\pi^2\frac{E\cdot I}{L^2}=\frac{\pi^2E\cdot b\cdot t^3}{3L^2}$
Maximum angle:
$\theta_{ref}=2\frac{\sigma_{max}\cdot L}{E\cdot t}$
The equivalent rolling radius of an orthogonal cross spring pivot is given by:
$\frac{\rho}{L}=-\frac{\sqrt2}{30}\left(36\left(a-0.5\right)^2-5\right)$
For $\frac{\rho}{L}<0$ the virtual rolling surface flips in relation to real mounting surface of the springs (see ‘Haberland’ cross spring)
Classical double symmetric cross spring pivot
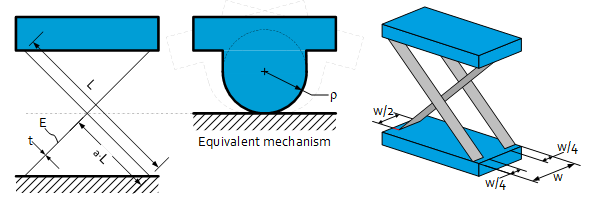
For $a=0.5$. Most often assembled from 3 separate plate spring elements with width $\frac{1}{4}w,\frac{1}{2}w,\frac{1}{4}w$. No pure pivot motion, but also parasitic displacement.
| ρ ⁄ L | 0.236 |
| Angular stiffness * | 0.5 • Kref |
| Buckle load * | 0.5 • Fbref |
| Maximum angle | θref |
*A factor 0.5 is included because the total width of the leaf springs is w, while in the reference situation this is 2w.
Special case classical double symmetric cross spring pivot
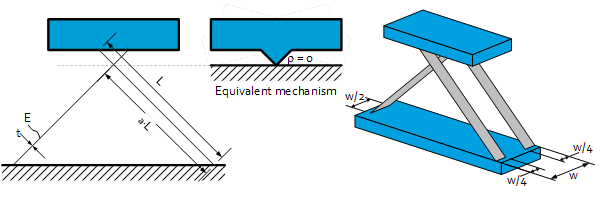
For $a=0.5\pm\frac{\sqrt5}{6}$. Special case classical double symmetric cross spring pivot where $\frac{\rho}{L}=0$ and thus pure pivot behavior.
| ρ ⁄ L | 0 |
| Angular stiffness * | 2.67 • Kref |
| Buckle load * | 0.5 • Fbref |
| Maximum angle | 1/3.3 • θref |
*A factor 0.5 is included because the total width of the leaf springs is w, while in the reference situation this is 2w.
‘Haberland’ cross spring pivot
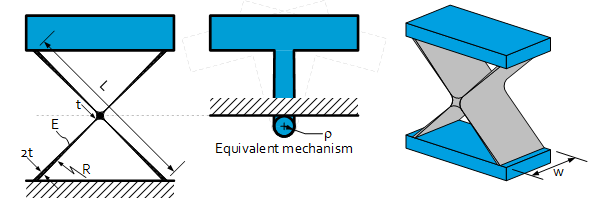
Ideally suited for monolithic fabrication. Relatively pure pivot behavior but with less angular stroke compared to classical double symmetric cross spring pivot.
| ρ ⁄ L * | -0.047 |
| Angular stiffness * | 4 • Kref |
| Buckle load * | Fbref |
| Maximum angle * | 1/4 • θref |
*Not according to reference equations due to coupled leaf springs.
