Introduction
This sheet is to do a quick scan to the resonances of a desired transfer of a dynamic system via state space approach. From state space a bode-diagram can be created with appropriate software.
Equations of Motion (n-dimensional)
$\underline{M}\ \underline{\ddot{x}}+\underline{D}\ \underline{\dot{x}}+\underline{K}\ \underline{x}+\underline{F}=\underline{0}$
with $\underline{x}=\left[\begin{matrix}x_1&\ldots&x_n\\\end{matrix}\right]^T\rightarrow n\ x\ 1$
$\underline{M}=\left[\begin{matrix}m_1&0&0&0\\0&m_2&0&0\\0&0&\ddots&0\\0&0&0&m_n\\\end{matrix}\right]\rightarrow n\ x\ n$
$\underline{K}=\left[\begin{matrix}K_{11}&K_{12}&\ldots&K_{1n}\\K_{21}&K_{22}&\ldots&K_{2n}\\\vdots&\vdots&\ddots&\vdots\\K_{n1}&K_{n2}&\ldots&K_{nn}\\\end{matrix}\right]\rightarrow n\ x\ n$
$K_{i,j}\rightarrow K_{mi, xj} =$ Sum of all $c$ that work on $m_i$ if $x_j$ is moved*
$\underline{D}=\left[\begin{matrix}D_{11}&D_{12}&\ldots&D_{1n}\\D_{21}&D_{22}&\ldots&D_{2n}\\\vdots&\vdots&\ddots&\vdots\\D_{n1}&D_{n2}&\ldots&D_{nn}\\\end{matrix}\right]\rightarrow n\ x\ n$
$D_{i,j}\rightarrow D_{mi, xj} =$ Sum of all $d$ that work on $m_i$ if $x_j$ is moved*
* Check for $\underline{K}$ and $\underline{D}$: If all elements of row or column $I$ are summed the result is the stiffness or damping of mass $I$ in relation to the fixed world (see example). Furthermore these matrices are
$\underline{F}= external force \rightarrow n\ x\ 1$
(not composed of stiffness/dampers)
State Space form (SISO, n-dimensional, time independent)
$\underline{\dot{q}}=\underline{A}\underline{q}+\underline{B}u $
$y=\underline{C}\underline{q}+\underline{D}u$
State vector: $\underline{q}=\left[\begin{matrix}x_1&\ldots&x_n\\\end{matrix}\ \ \begin{matrix}{\dot{x}}_1&\ldots&{\dot{x}}_n\\\end{matrix}\right]^T\rightarrow2n\ x\ 1$
$u= input \rightarrow1\ x\ 1$
$u$ should be at least $\frac{d}{dt}$ , so no $x_i$, always a flux or a multiplication of fluxes with parameters (see example).
$y= output\rightarrow1\ x\ 1$
$y$ should be in the form $x_i$ or ${\dot{x}}_i$ and multiplications with parameters are possible but no double flux or higher fluxes (see example).
$\underline{A}=\left[\begin{matrix}\underline{0}_{nxn}&\underline{I}_{nxn}\\{\underline{M}}^{-1}\underline{K}&\underline{M}^{-1}\underline{D}\end{matrix}\right]→2n\ x\ 2n$ (system matrix)
$\underline{B}\rightarrow2n\ x\ 1$ is the input matrix; composition see examples
$\underline{C}\rightarrow2n\ x\ 1$ is the output matrix; composition see examples
This document assumes no feed forward so: $\underline{D}=\underline{0}$
Block diagram representation
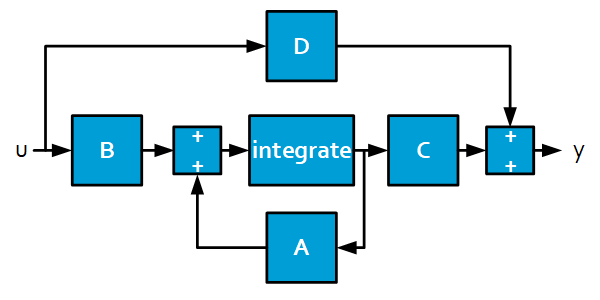
Example
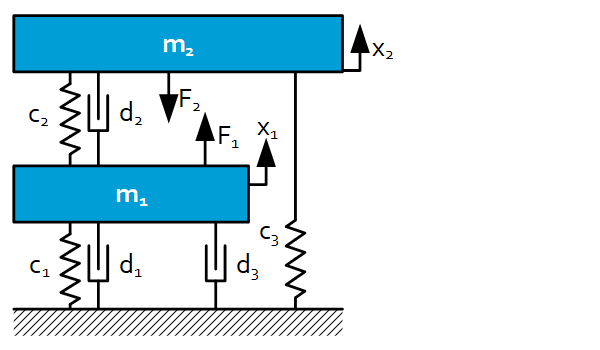
$\underline{x}=\left[\begin{matrix}x_1&x_2\\\end{matrix}\right]^T$ so: $n=2 $
$\underline{M}=\left[\begin{matrix}m_1&0\\0&m_2\\\end{matrix}\right]$ with $m_0=0$
$\underline{K}=\left[\begin{matrix}-c_1-c_2&c_2\\c_2&-c_2-c_3\\\end{matrix}\right]$
$\underline{D}=\left[\begin{matrix}-d_1-d_2-d_3&d_2\\d_2&-d_2\\\end{matrix}\right]$
$\underline{F}= \left[{\ F}_1\ -F_2\right]$
$\underline{q}=\left[\begin{matrix}x_1&x_2&{\dot{x}}_1&{\dot{x}}_2\\\end{matrix}\right]^T$
$\underline{A}=\left[\begin{matrix}\begin{matrix}0&0\\0&0\\\end{matrix}&\begin{matrix}1&0\\0&1\\\end{matrix}\\{\underline{M}}^{-1}\underline{K}&{\underline{M}}^{-1}\underline{D}\\\end{matrix}\right]$ with $M^{-1}=\left[\begin{matrix}1/m_1&0\\0&1/\ m_2\\\end{matrix}\right]$
3 examples of inputs:
$u_1={\ddot{x}}_1$, $u_2=F_1$, $u_3={\dot{x}}_2-{\dot{x}}_1$
Thus;
${\underline{B}}_1=\left[\begin{matrix}0&0&1&0\\\end{matrix}\right]^T $
${\underline{B}}_2=\left[\begin{matrix}0&0&\frac{1}{m_1}&0\\\end{matrix}\right]^T$
${\underline{B}}_3=\left[\begin{matrix}-1&1&0&0\\\end{matrix}\right]^T$
3 examples of outputs:
$y_1={\dot{x}}_2$, $y_2=x_2-x_1$, $y_3=c_2\left(x_2-x_1\right)+d_2({\dot{x}}_2-{\dot{x}}_1)$
Thus;
${\underline{C}}_1=\left[\begin{matrix}0&0&0&1\\\end{matrix}\right]^T $
${\underline{C}}_2=\left[\begin{matrix}-1&1&0&0\\\end{matrix}\right]^T $
${\underline{C}}_3=\left[-\begin{matrix}c_2&c_2&-d_2&d_2\\\end{matrix}\right]^T$
$\underline{D}=\underline{0}$
