Introduction
Method to derive a best fit of a sphere through a number (≥ 4) of XYZ data points, where the summed square errors of the data points in relation to the fit-sphere are in the direction perpendicular to the surface.
Equation of a sphere
$z\left(x,y\right)=\sqrt{\left(R^2-\left(x-x_c\right)^2-\left(y-y_c\right)^2\right)}+z_c$
$\left(x_c,\ y_c,z_c\right)$ is the location of the center of the sphere, and $R$ is the radius of the sphere.
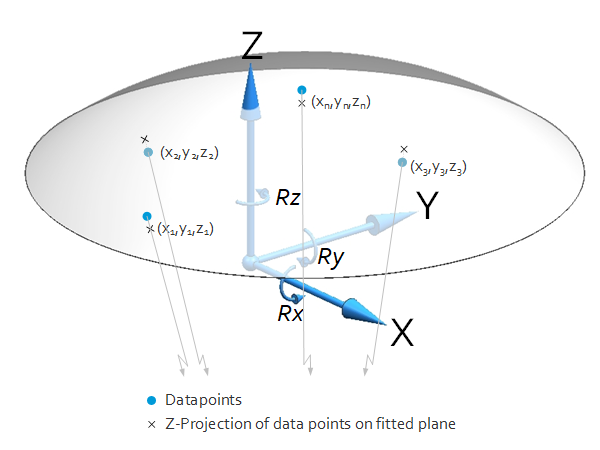
Data points
$\left[\begin{matrix}x_1&y_1&z_1\\x_2&y_2&z_2\\x_3&y_3&z_3\\x_3&y_4&z_4\\&\vdots&\\x_n&y_n&z_n\\\end{matrix}\right]$
Center location and radius of fitted sphere
$A=2\cdot\left[\begin{matrix}\sum_{i=1}^{i=n}\frac{x_i\cdot\left(x_i-\bar{x}\right)}{n}&\sum_{i=1}^{i=n}\frac{x_i\cdot\left(y_i-\bar{y}\right)}{n}&\sum_{i=1}^{i=n}\frac{x_i\cdot\left(z_i-\bar{z}\right)}{n}\\\sum_{i=1}^{i=n}\frac{y_i\cdot\left(x_i-\bar{x}\right)}{n}&\sum_{i=1}^{i=n}\frac{y_i\cdot\left(y_i-\bar{y}\right)}{n}&\sum_{i=1}^{i=n}\frac{y_i\cdot\left(z_i-\bar{z}\right)}{n}\\\sum_{i=1}^{i=n}\frac{z_i\cdot\left(x_i-\bar{x}\right)}{n}&\sum_{i=1}^{i=n}\frac{z_i\cdot\left(y_i-\bar{y}\right)}{n}&\sum_{i=1}^{i=n}\frac{z_i\cdot\left(z_i-\bar{z}\right)}{n}\\\end{matrix}\right]$
$B=\left[\begin{matrix}\sum_{i=1}^{n}\frac{\left(x_i^2+y_i^2+z_i^2\right)\cdot\left(x_i-\bar{x}\right)}{n}\\\sum_{i=1}^{n}\frac{\left(x_i^2+y_i^2+z_i^2\right)\cdot\left(y_i-\bar{y}\right)}{n}\\\sum_{i=1}^{n}\frac{\left(x_i^2+y_i^2+z_i^2\right)\cdot\left(z_i-\bar{z}\right)}{n}\\\end{matrix}\right]$
$\bar{x}=\frac{1}{n}\sum_{i=1}^{i=n}x_i,\ \ \ \ \ \bar{y}=\frac{1}{n}\sum_{i=1}^{i=n}y_i,\ \ \ \ \ \bar{z}=\frac{1}{n}\sum_{i=1}^{i=n}z_i$
$\left[\begin{matrix}x_c\\y_c\\z_c\\\end{matrix}\right]=\left(A^T\cdot A\right)^{-1}\cdot A^T\cdot B$
$R=\sqrt{\frac{\sum_{i=1}^{i=n}\left(\left(x_i-x_c\right)^{2\ }+\left(y_i-y_c\right)^{2\ }+\left(z_i-z_c\right)^{2\ }\right)}{n}}$
Fit quality – Coefficient of determination = R2
$R^2=1-\frac{\sum_{i=1}^{i=n}\left(z_i-z\left(x_i,y_i\right)\right)^2}{\sum_{i=1}^{i=n}\left(z_i-\frac{1}{n}\sum_{i=1}^{n}z_i\right)^2}$
A value of $R^2$ which is close to 1 indicates a good fit quality.