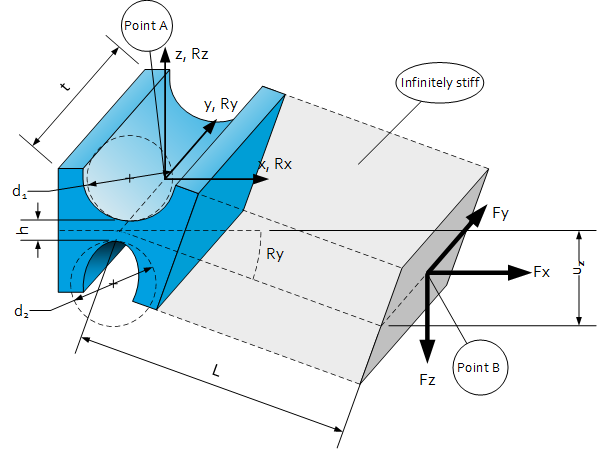
Stiffness at point A
$D=\frac{2d_1d_2}{d_1+d_2}, D(d_2=\infty)=2d_1$ (straight, see below)
$C_{Ax}=0.48Et\sqrt{\frac{h}{D}}$
${C_A}_y^\ast>\frac{GA}{l}=\frac{Ght}{D}=\frac{Eht}{2D(1+\nu)}$
*No acknowledged equation. Above stated equation can only be used as a rough estimate
$C_{Az}=0.56Et\sqrt{\frac{h}{D}}\left(\frac{1}{1.2+{\frac{D}{h}}}\right)$
$K_{Ax}=\frac{1}{12}t^2\cdot\ C_z=0.047Et^3\sqrt{\frac{h}{D}}\left(\frac{1}{1.2+{\frac{D}{h}}}\right)$
$K_{Ay}=0.093Eth^2\sqrt{\frac{h}{D}} $
$K_{Az}= \frac{1}{12}t^2\cdot\ C_x=0.04Et^3\sqrt{\frac{h}{D}}$
Stiffness at point B
$C_{Bx}=C_{Ax} $
$\frac{1}{C_{By}}\ =\frac{1}{C_{Ay}}+\frac{L^2}{K_{Az}}\ \ \ \ \ C_{BY}=\frac{C_{Ay}K_{Az}}{K_{Az}+C_{Ay}L^2}$
$\frac{1}{C_{Bz}}=\frac{1}{C_{Az}}+\frac{L^2}{K_{Ay}}\ \ \ \ \ C_{BZ}=\frac{C_{Az}K_{Ay}}{K_{Ay}+C_{Az}L^2}$
Other properties
$u_z=\frac{F_z}{C_{Bz}}$
$R_y=\frac{F_zL}{K_{Ay}}$
$\sigma_{max}\approx0.58E\sqrt{\frac{h}{D}}R_y=ES\cdot R_y$
Version with equal $h$, $C_x$ and $K_y$
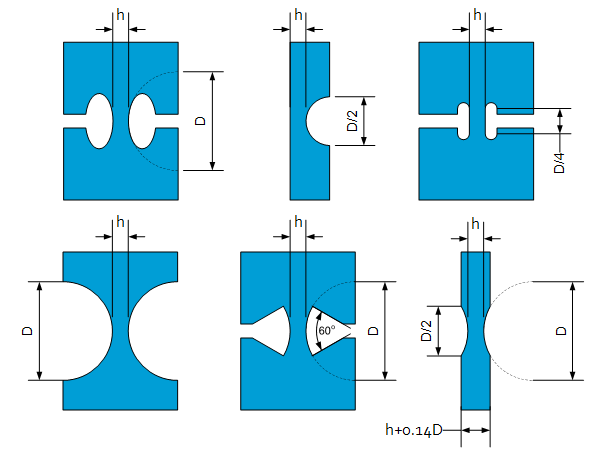
Design rules of thumb
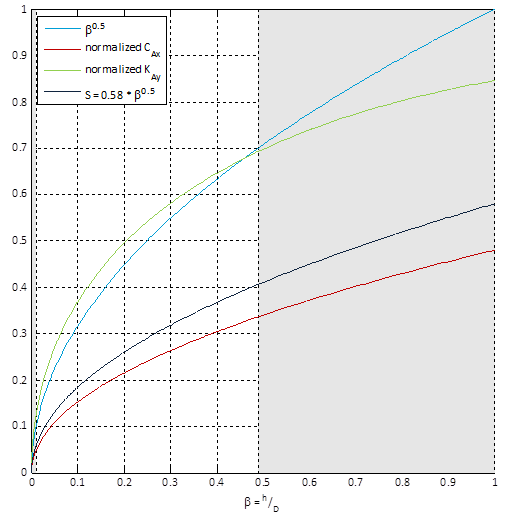
Elastic hinge parameter: $\beta=\frac{h}{D}$
Realistic area: $0.01<\beta<0.5$
$\beta<0.01$ : manufacturability
$\beta>0.5$ : hinge functionality gone
Trade-off between:
Maximum $C_{Ax}: \beta=0.5$
Minimum $K_{Ay}: \beta=0.01$
Normalized:
$C_{Ax\ norm}=0.48\sqrt\beta$
$K_{Ay\ norm}=1.3\sqrt\beta-0.42\beta-0.034\beta^{1.5}$
$S=0.58\sqrt\beta$