Introduction
Bodies collide e.g. when play is present in the design. This collision causes elastic or plastic deformations to the colliding bodies.
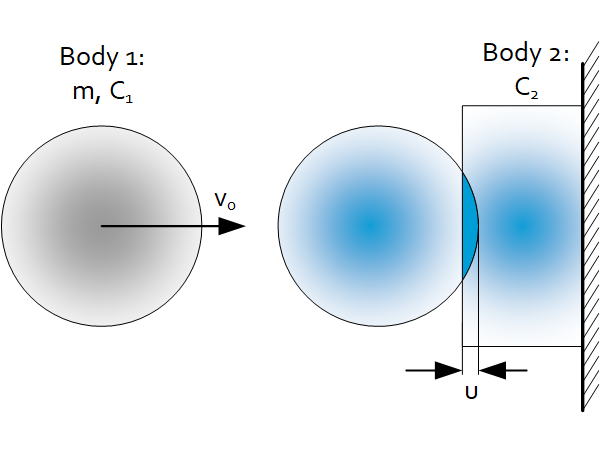
Collision Stiffness
If both are ‘rigid’ take the local Hertzian stiffness.
$c=\frac{C_1C_2}{C_1+C_2}$
Max. Collision Force
$F=v_0\sqrt{mc}$
Max. Approach
$u=v_0\sqrt{\frac{m}{c}}$
Deceleration Time
$t=\frac{\pi}{2}\sqrt{\frac{m}{c}} $
Deceleration to $v=0$
${a_{max}=-v}_0\sqrt{\frac{c}{m}}$
$a_{ave}=-\frac{v_0}{t}=-\frac{2}{\pi}v_0\sqrt{\frac{c}{m}}$
Collision of bodies
Differential Equation:
$m\ddot{x}+cx=0$
$x\left(t\right)=k_1\cos{\left(\sqrt{\frac{c}{m}}t\right)}+k_2\sin{\left(\sqrt{\frac{c}{m}}t\right)}$
Coefficients:
$x\left(0\right)=k_1=0$
$v\left(0\right)=k_2\sqrt{\frac{c}{m}}=v_0$ with $k_2=v_0\sqrt{\frac{m}{c}}$
Distance, velocity, and acceleration:
$x\left(t\right)=v_0\sqrt{\frac{m}{c}}\sin{\left(\sqrt{\frac{c}{m}}t\right)} $
$v\left(t\right)=v_0\cos{\left(\sqrt{\frac{c}{m}}t\right)}$
$a\left(t\right)={-v}_0\sqrt{\frac{c}{m}}\sin{\left(\sqrt{\frac{c}{m}}t\right)}$
