Introduction
This sheet gives some insight about stiffness and damping and their effect on the dynamics of mechanical systems.
Influence of stiffness
Stiffness increases the tracking behavior the displacement x of the end-effector (mass m) in relation to the input $x_{in}$ (a stiff actuator). Moreover, it decreases the influence of the external force $F_e$, which is often a disturbance to the system.
Influence of damping
Damping is difficult! Damping can be regarded as loss of energy. However, the positive effect of damping is that it damps oscillations and resonances.
Damping prediction
The damping of mechanical systems is hard to predict. Rule of thumb: damping decreases with increasing frequency. Joints and other system impurities increase damping.
$d=2\zeta\sqrt{cm}$ with viscous damping ratio $\zeta$:
| System | ζ [-] |
|---|---|
| Metals in elastic range | 0.01 |
| Continuous metal structures | 0.02 - 0.04 |
| Metal structures with joints | 0.03 - 0.07 |
| Plastics (hard - soft) | 0.02 - 0.05 |
| Rubber | 0.05 |
| Sintered material (piezos) | 0.05 |
| Airpots (vibration isolation tables) | 0.07 |
Schematic overview
1 mass $m$, 1 spring $c$, 1 damper $d$, input $x_{in}$ , external force $F_e$
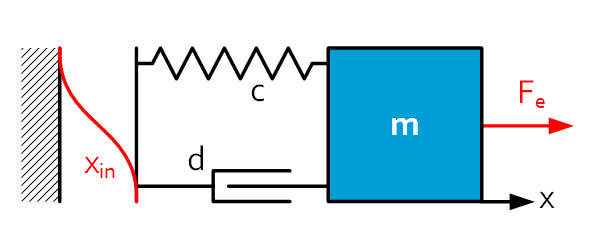
Differential equation
$m\ddot{x}+d({\dot{x}-\dot{x}}_{in})+c(x-x_{in})=F_e$
Tracking – design rule
When designing a system that has to track the input $x_{in}$ and that needs to be insensitive to disturbance force $F_e$, then design ‘light and stiff’.
Vibration isolation – design rule
When designing a system that needs to be insensitive to vibrations $x_{in}$ (such as ground vibrations), then design ‘heavy and soft’.
Eigen frequency
At this point the spring energy is converted into kinetic energy: $cx=m\ddot{x}$ hence: $c\hat{x}=m{\hat{x}\omega}^2$ and thus: $\omega=\sqrt{c/m}$
Response to the external force: $H_1=\frac{x}{F_e}=\frac{1}{ms^2+ds+c}$
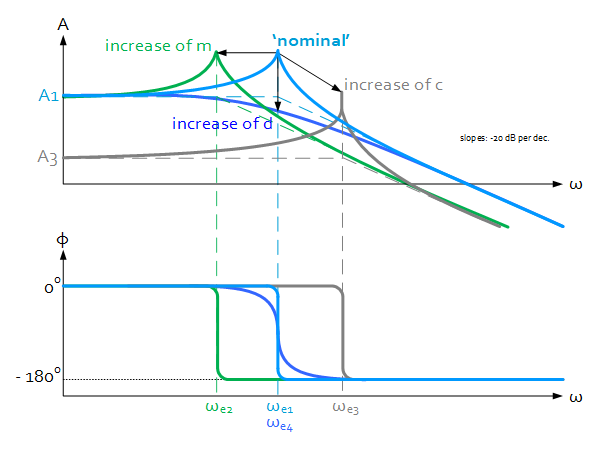
Properties:
- Eigen frequency: $\omega_{ei}=\sqrt{\frac{c}{m}}\sim\sqrt c\sim\frac{1}{\sqrt m}$
- Gain at $\omega=0 : A_i=\frac{1}{c}\sim\frac{1}{c}$
Response to the input: $H_1=\frac{x}{F_e}=\frac{ds+c}{ms^2+ds+c}$
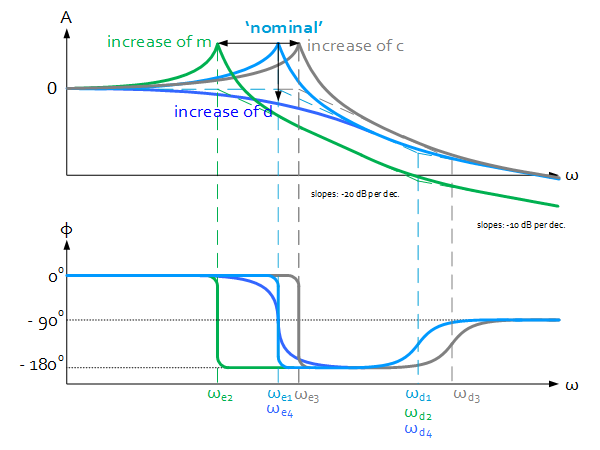
Properties:
Eigen frequency: $\omega_{ei}=\sqrt{\frac{c}{m}}\sim\sqrt c\sim\frac{1}{\sqrt m}$
2nd cross-over frequency: $\omega_{ei}=\frac{c}{d}\sim c\sim\frac{1}{d}$
(from $cx=d\dot{x}$ hence: $c\hat{x}=d\hat{x}\omega$ and thus: $\omega=c/d$ )Gain at $\omega=0$ : $A_i=\frac{c}{c}\ =1=0\ dB$
