Introduction
The mass moment of inertia measures the extent to which an object resists rotational acceleration about a particular axis, and is the rotational analogue to mass. The torque needed to achieve an angular acceleration is defined by:
$$T=I\dot{\omega}$$
The mass moment of inertia for several shapes is shown in the table below.
| Figure | Description | Mass moment of inertia |
|---|---|---|
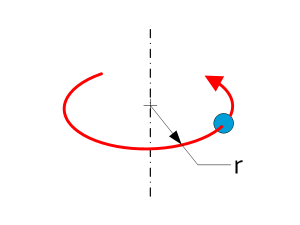 | Point mass | $$I=mr^2$$ |
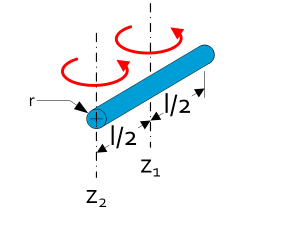 | Rod of length l and mass m | With l>>r $$I_{z1}=\frac{1}{12}ml^2$$ $$I_{z2}=\frac{1}{3}mL^2$$ |
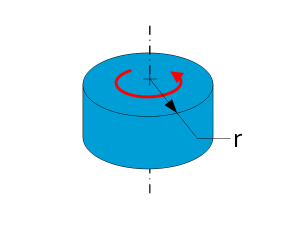 | Solid cylinder | $$I=\frac{1}{2}mr^2$$ |
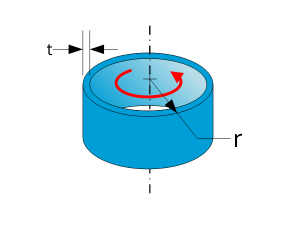 | Cylindrical shell | With r>>t $$I=mr^2$$ |
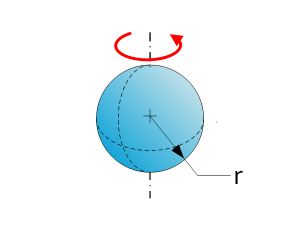 | Sphere | $$I=\frac{2}{5}mr^2$$ |
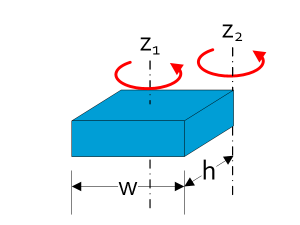 | Block | $$I_{z1}=\frac{1}{12}m\left(w^2+h^2\right)$$ $$I_{z2}=\frac{1}{3}m\left(w^2+h^2\right)$$ |
