Introduction
Designing an actuator that utilizes a piezo stack as actuation principles is not trivial. To aid in this, this sheet elaborates on the parameters that are of interest for such a design. The behavior of a piezo stack can be summarized with the following properties:
- Geometrical
- Material
- Mechanical
- Electrical
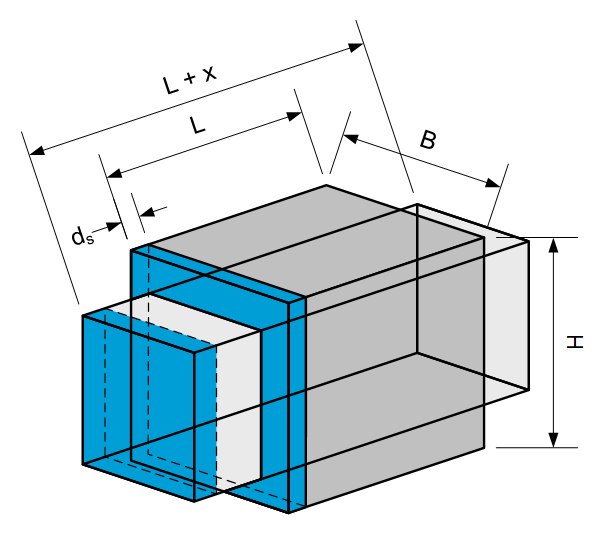
Geometric properties
$A=H\cdot B\left[m^2\right]$
Cross section area
$d_s[m]$
Layer thickness (typical 60-500 µm)
$n=\frac{L}{d_s} [-]$
Number of layers
Material properties
$\rho=7.8e3\frac{kg}{m^3}$
Density
$E=36e9\frac{N}{m^2}$
Young’s modulus
$\nu=0.34$
Poisson ratio
$\xi=0.1$
Damping constant
(estimate)
$-{271}^oC<T<{150}^oC$
Operating temperature
$\varepsilon_{33}=300-4000$
Dielectric constant (typical value = 1750)
$d_{33}=4e-10\frac{m}{V}$
Charge constant
$HC=350\frac{J}{kg\cdot K}$
Spec. heat capacity
$TC=1.1\frac{W}{mK}$
Spec. thermal conductivity
$-20V<U<120V$
Typical voltage
Mechanics
$\Delta L_{max}=\frac{L}{1000}$
Maximum displacement
$C_{axial}=\frac{EA}{L}$
Axial stiffness
$D=2\xi\sqrt{C_{axial}m}$
Damping
$f_0=\frac{1}{2\pi}\sqrt{\frac{C_{axial}}{m}}$
Resonance frequency
$t_{min}=\frac{1}{3f_0}$
Minimum rise time
$\varphi=2\arctan{\left(\frac{f}{f_0}\right)}$
Phase lag
$F_{blocking}=\Delta l_{max}\cdot C_{axial}$
Blocking force
$\sigma_{dynamic}=15\ MPa$
Preload for dynamic use
$\sigma_{static}=30\ MPa$
Preload for static use
$4-20 \%$
Hysteresis
$\Delta x_{creep}\left(t\right)=x\cdot0.01\cdot\log{\left(\frac{t}{0.1}\right)}$
Creep @ t [s]
$F_{pre\ tension}=\frac{1}{2}F_{blocking}$
Pre tension force (matching push-pull force)
Electronics
$x=d_{33}\cdot L\cdot\frac{U}{d_s}$
Displacement @ U [V]
$\varepsilon_0=8.9e-12\frac{F}{m}$
Permittivity of free space
$C_S=n\cdot\varepsilon_0\cdot\varepsilon_{33}\cdot\frac{A}{d_s}$
Small signal capacitance (typical for U < 100 V)
$C_L=1.7\cdot C_S$
Large signal capacitance (typical for U > 100 V)
$P=\frac{1}{2}\cdot f\cdot C\cdot U^2$
Average Polarization Power
$E=\frac{1}{2}\cdot C\cdot U^2$
Polarization energy
Not generic for all frequency ranges, just for indication:
$\tan{\delta_U}=0.015+0.016\sqrt{\frac{U}{\left[V\right]}}$
Loss factor @ U [V]
$\tan{\delta_T}=0.28+0.17\cdot\ln{\left(\frac{T}{\left[K\right]}\right)}$
Loss factor @ T [K]
$\tan{\delta}=\tan{\delta_U}+\tan{\delta_T}$
Heat generation
$P_{heat}=P\cdot\tan{\delta}$
Heat generation
