Introduction
Various shapes can be used as a spring to provide certain stiffness. Below several shapes are described. Also the stroke according to the maximum occurring stress in the particular shape is added; maximum stroke at yield stress.
$$\tau_{0.2}\approx0.4\cdot\sigma_{0.2} \textsf{ (JPE estimate for metals)}$$
Below materials are characterized with: $E,\sigma_{0.2},\nu$

| Spring type | Equations |
|---|---|
Buckled plate / wire spring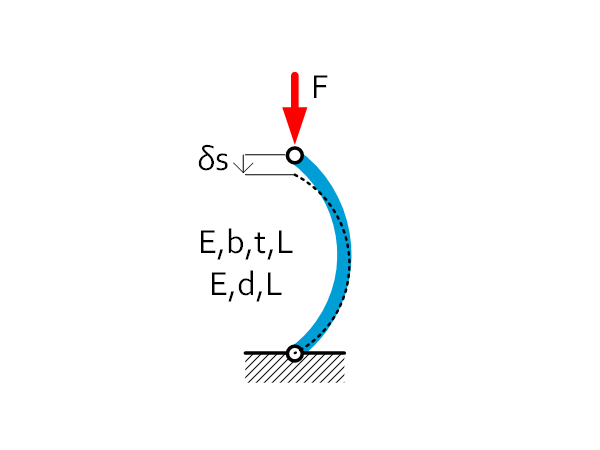 | $F_{buckling}=\frac{\pi^2EI}{L^2}=\frac{\pi^2Ebt^3}{12L^2} $ $F_{buckling}=\frac{\pi^2EI}{L^2}=\frac{\pi^3Ed^4}{64L^2} $ $C\approx0$ (Constant force F) $\delta\ s_{max}=\ (not\ known) $ |
Torsion wire spring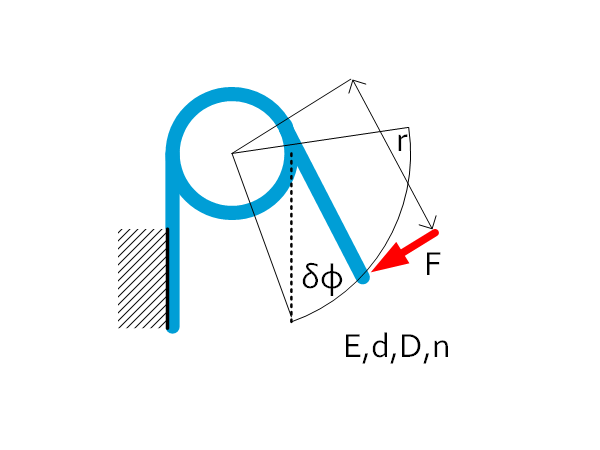 | $M=Fr $ $K=\frac{M}{\delta\varphi}=\frac{Ed^4}{64nD} $ $\delta\varphi=\frac{2\pi nD}{Ed}\sigma $ |
Spiral plate / wire spring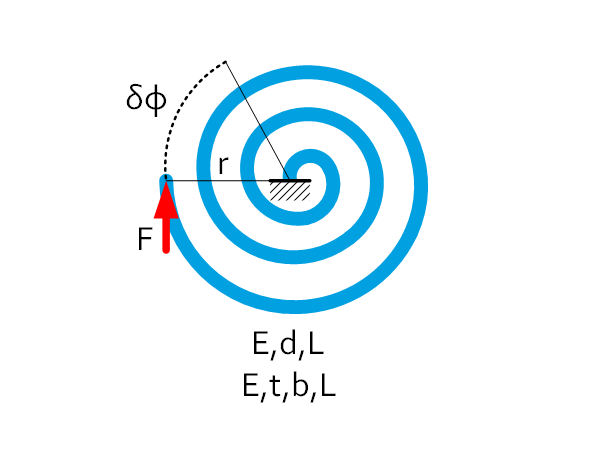 | $M=Fr $ $K=\frac{M}{\delta\varphi}=\frac{Ebt^3}{12L} $ $K=\frac{M}{\delta\varphi}=\frac{\pi Ed^4}{64L} $ $\delta\varphi=\frac{2L}{Et}\sigma $ $\delta\varphi=\frac{2L}{Ed}\sigma $ |
Disc spring (DIN 2092)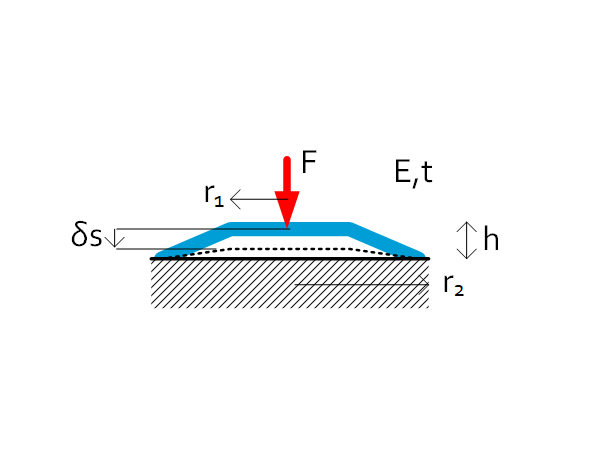 | $r_1=\frac{r_2}{2} $ $C=\frac{F}{\delta s}=\frac{Et^3}{0.69{r_2}^2\left(1-\nu^2\right)} $ $\delta s_{max}=h $ |
Compression / tension spring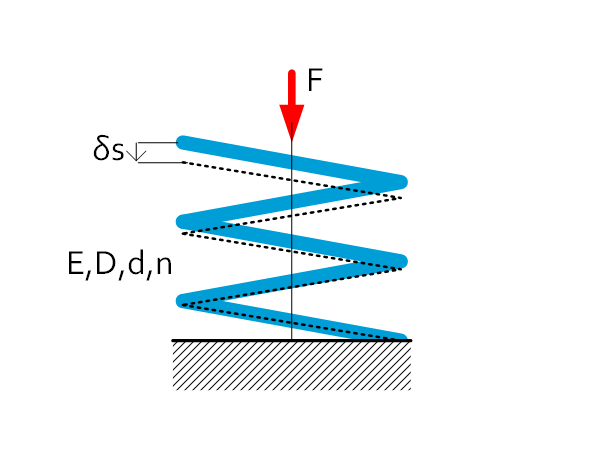 | $C=\frac{F}{\delta s}=\frac{d^4E}{16nD^3(1+\nu)} $ $\delta s=\frac{2\pi n D^2\left(1+\nu\right)}{dE}\tau $ |
Inclined compression spring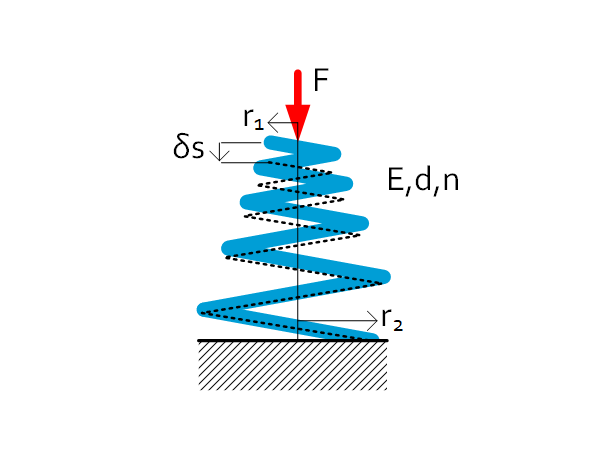 | $C=\frac{F}{\delta s}=\frac{d^4E}{32n(r_1+r_2)(r_1^2+r_2^2)(1+\nu)} $ $\delta s=\frac{2\pi n(r_1+r_2)(r_1^2+r_2^2)\left(1+\nu\right)}{dr_2E}\tau $ |
Ring plate / wire spring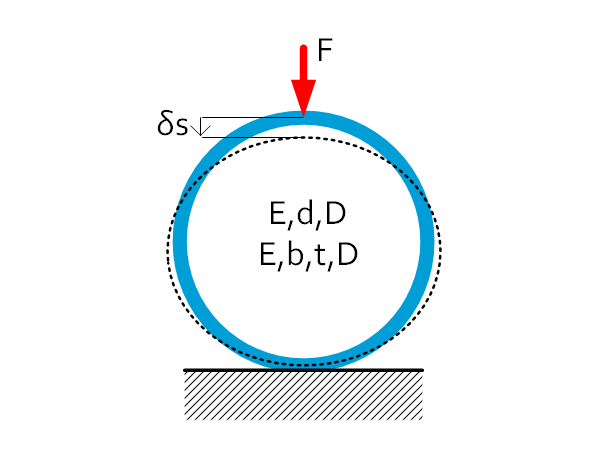 | $C=\frac{F}{\delta s}=4.48\frac{Ebt^3}{D^3(1-\nu^2)} $ $C=\frac{F}{\delta s}=2.64\frac{Ed^4}{D^3(1-\nu^2)} $ $\delta s=\frac{\pi D^2}{13.44Et}\sigma$ $\delta s=\frac{\pi D^2}{13.44Ed}\sigma$ |
Plate / wire spring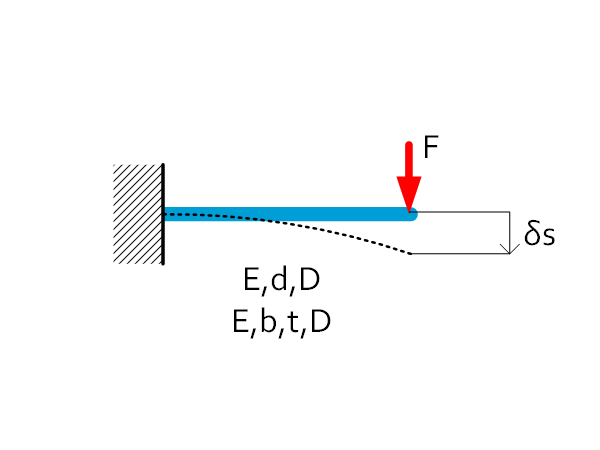 | $C=\frac{3EI}{L^3}=\frac{Ebt^3}{4L^3} $ $C=\frac{3EI}{L^3}=\frac{3\pi E\ d^4}{64L^3} $ $\delta s=\frac{4L^2}{3Et}\sigma $ $\delta s=\frac{4L^2}{3Ed}\sigma $ |
