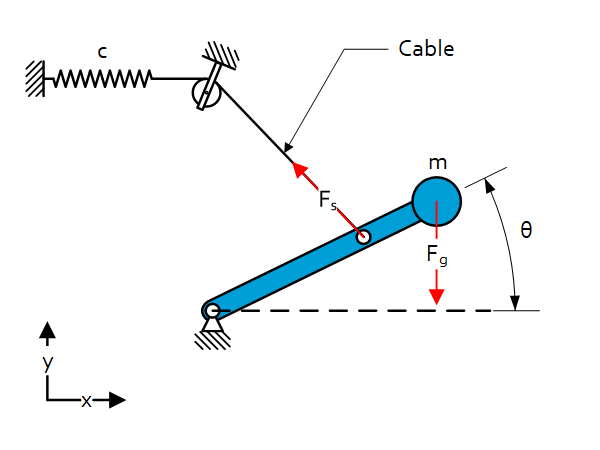
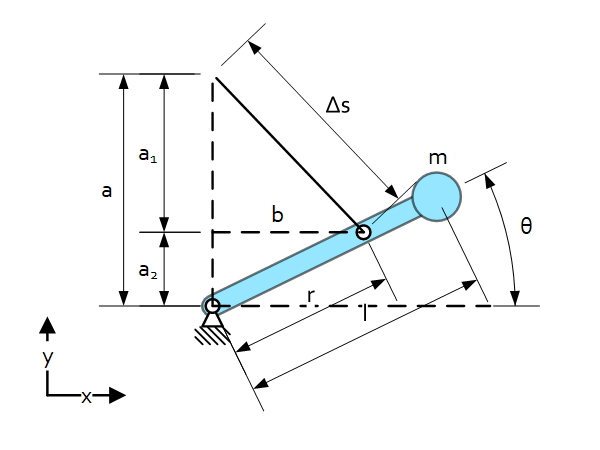
Introduction
Statically balanced mechanisms are used to compensate for the gravity force of masses. Allowing these mechanisms to move from one configuration to another without the need for large actuation forces. This gravity compensation is done by using springs.
Static equilibrity equation
To have a static equilibrium the sum of all forces has to be zero. A statically balanced mechanism goes one step further by having a static equilibrium in multiple configurations ($0^{\circ}\leq \Theta\leq 360^{\circ}$ in this case).
Potential energy equation
$U_t=U_m+U_s$
$U_m=mgh=mgl\sin{\theta}$
$U_s=\frac{c\cdot\Delta s^2}{2}$
Spring elongation
$a_2=r\sin{\theta} $
$a_1=a-a_2=a-r\sin{\theta} $
$b^2=r^2-a_2^2=r^2-\ r^2\sin^2{\theta} $
$\Delta s^2=a_1^2+b^2=a^2+r^2-2ar\sin{\theta}$
Potential energy of spring
$U_s=\frac{c}{2}\left(a^2+r^2-2ar\sin{\theta}\right) $
$U_t=mgl\sin{\theta}+\frac{c}{2}\left(a^2+r^2-2ar\sin{\theta}\right)$
$U_t=\left(mgl-car\right)\sin{\theta}+\frac{c}{2}\left(a^2+r^2\right) $
$U_t=\left(mgl-car\right)\sin{\theta}+constant$
By tuning $m,l,c,a$ and $r$ so that $mgl=car$, $U_t$ will be constant and independent of $\theta$. This means that the mechanism will be statically balanced at every value of $\theta$. During variation of $\theta$, no force has to be applied (except for friction forces) to move the mechanism.