Introduction
In many mechatronic applications where a movement from A to B needs to be performed, a third order point to point motion profile is used.
To enable early insight in the relevant parameters of a motion profile it is useful to calculate and visualize the relevant parameters (position, speed, acceleration and jerk).
This sheet provides analytical formulas to calculate the quickest motion between point A to point B based on given maximum levels speed, acceleration and jerk.
Approach
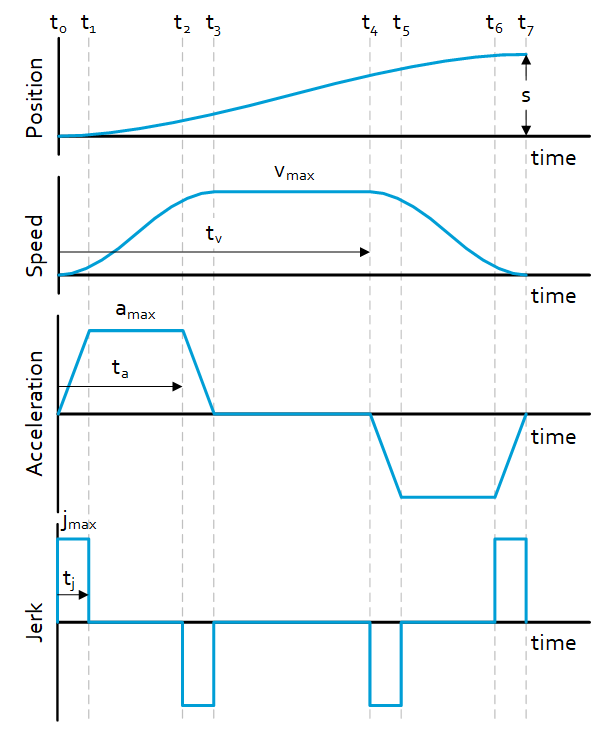
The typical time plot of the parameters of a third order profile is depicted on the right.
The difficulty in defining the motion trajectory is that the shape is not always the same. For example, there are cases where the maximum speed or acceleration level is not achieved, because there is not enough time to build up to the maximum before slowing down again. There are 6 different trajectory shapes that influence the motion profile.
The approach to find your motion profile is as follows:
- Define which trajectory shape you have (I … VI) by comparing your required distance $s$ and maximum velocity $v_{max}$ with $s_v,\ s_a$ and $v_a$ (which are based on $J_{max},\ a_{max}$ and $v_{max}$).
- Calculate the characteristic time intervals $t_j,\ t_a,\ t_v$ based on your trajectory shape (I … VI).
- Translate the characteristic time intervals to the $t_1\ldots t_7$ values.
- Using the formula’s in the Motion parameters table the curves for jerk, acceleration, velocity and position on each time interval can be calculated.
| 1. Trajectory shape | I | II | III | IV | V | VI | |
|---|---|---|---|---|---|---|---|
| $v_{max}$ | < | > | < | < | > | > | $v_a=\frac{{a_{max}}^2}{j_{max}}$ |
| $s$ | > | < | < | < | > | > | $s_a=\frac{2\cdot{a_{max}}^3}{{j_{max}}^2}$ |
| > | < | > | < | $s_v=v_{max}\left[M\left(2\sqrt{\frac{v_{max}}{j_{max}}}\right)+N\left(\frac{v_{max}}{a_{max}}+\frac{a_{max}}{j_{max}}\right)\right]$ $M=1,N=0\ \textsf{if}\ v_{max}j_{max}<{a_{max}}^2$ $M=0,N=1\ \textsf{if}\ v_{max}j_{max}\geq{a_{max}}^2$ |
| 2. Characteristic time intervals | ||||||
|---|---|---|---|---|---|---|
| Trajectory shape | I | II | III | IV | V | VI |
| $t_j$ | $\sqrt{\frac{v_{max}}{j_{max}}}$ | $\sqrt[3]{\frac{s}{{2\cdot j}_{max}}}$ | $\sqrt{\frac{v_{max}}{j_{max}}}$ | $\sqrt[3]{\frac{s}{{2\cdot j}_{max}}}$ | $\frac{a_{max}}{j_{max}}$ | $\frac{a_{max}}{j_{max}}$ |
| $t_a$ | $t_j$ | $t_j$ | $t_j$ | $t_j$ | $\frac{v_{max}}{a_{max}}$ | $\frac{1}{2}\left(\sqrt{\frac{4\cdot s\cdot{j_{max}}^2+{a_{max}}^3}{a_{max}\cdot{j_{max}}^2}}-\frac{a_{max}}{j_{max}}\right)$ |
| $t_v$ | $\frac{s}{v_{max}}$ | $2\cdot t_j$ | $\frac{s}{v_{max}}$ | $2\cdot t_j$ | $\frac{s}{v_{max}}$ | ${t_a+t}_j$ |
| 3. Time intervals as function of characteristic time intervals | |
|---|---|
| t1 = tj | t5 = tv + tj |
| t2 = ta | t6 = tv + ta |
| t3 = ta + tj | t7 = tv + tj + ta |
| t4 = tv | |
| 4. Motion parameters | jerk | acceleration | velocity | position | |||
|---|---|---|---|---|---|---|---|
| t0…t1 | jmax | jmax ∙ (t - t0) | 1/2 ∙ jmax ∙ (t - t0)2 | 1/6 ∙ jmax ∙ (t - t0)3 | |||
| t1…t2 | 0 | a1 = a2 | v1 + a1 ∙ (t - t1) | p1 + v1 ∙ (t - t1) + 1/2 ∙ a1 ∙ (t - t1)2 | |||
| t2…t3 | -jmax | a2 - jmax ∙ (t - t2) | v2 + a2 ∙ (t - t2) + 1/2 ∙ -jmax ∙ (t - t2)2 | p2 + v2 ∙ (t - t2) + 1/2 ∙ a2 ∙ (t - t2)2 + 1/6 ∙ - jmax ∙ (t - t2)3 | |||
| t3…t4 | 0 | 0 | v3 = v4 | p3 + v3 ∙ (t - t3) | |||
| t4…t5 | -jmax | -jmax ∙ (t - t4) | v4 + 1/2 ∙ - jmax ∙ (t - t4)2 | p4 + v4 ∙ (t - t4) + 1/6 ∙ - jmax ∙ (t - t4)3 | |||
| t5…t6 | 0 | a5 = a6 | v5 + a5 ∙ (t - t5) | p5 + v5 ∙ (t - t5) + 1/2 ∙ a5 ∙ (t - t5)2 | |||
| t6…t7 | jmax | a6 + jmax ∙ (t - t6) | v6 + a6 ∙ (t - t6) + 1/2 ∙ jmax ∙ (t - t6)2 | p6 + v6 ∙ (t - t6) + 1/2 ∙ a6 ∙ (t - t6)2 + 1/6 ∙ jmax ∙ (t - t6)3 | |||
