Introduction
Zernike modes are an infinite series of polynomials that can be used to describe surface shapes on the unit disk. They are often used in optics to describe and quantify wavefront aberrations in mirrors and lenses with a circular aperture.
Definition
Zernike polynomials are defined in a polar coordinate system with radius $\rho$ and angle $\varphi$. Each Zernike polynomial $Z_n^m(\rho,\varphi)$ is uniquely defined by its radial order $n$ and angular order $m$.
$$Z_n^m\left(\rho,\varphi\right)=N_n^m\cdot\ R_n^m\left(\rho\right)\cdot\ A^m\left(\varphi\right)\cdot\ z_n^m$$
$N_n^m$
$R_n^m\left(\rho\right)$
$A^m\left(\varphi\right)$
$z_n^m$
Normalization term
Radial polynomial
Angular term
Zernike coefficient
Each mode consists of an $n^{th}$ order polynomial over the radius of the unit disk. This polynomial is multiplied with a sinusoidal term to obtain a surface shape of a given mode:
$$R_n^m\left(\rho\right)=\ \sum_{k=0}^{\frac{n-m}{2}}\frac{\left(-1\right)^k\left(n-k\right)!}{k!\left(\frac{n+m}{2}-k\right)!\left(\frac{n-m}{2}-k\right)!}\rho^{n-2k}$$
$$A^m\left(\varphi\right)=\left\{\begin{matrix}\cos{\left(m\varphi\right)};for\ m\geq0\\\sin{\left(m\varphi\right)};for\ m<0\\\end{matrix}\right\}$$
The normalization term $N_n^m$ gives each Zernike mode an RMS value equal to $z_n^m$.
$$N_n^m=\ \sqrt{\frac{2\left(n+1\right)}{1+\delta_{m0}}}$$
With $\delta_{m0}$ the Kronecker delta function, which is $1$ for $m=0$ and $0$ in all other cases. The Zernike coefficient $z_n^m$ defines the magnitude of the given mode. The double indexing is often replaced by a single index according to the Noll or Wyant expansion schemes.
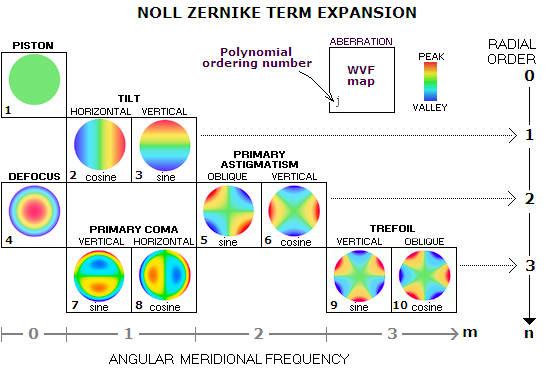
Describing wave fronts
Much like a Fourier transform, any wave front shape can be described by the sum of an infinite number of Zernike polynomials. A vector $z$ containing the Zernike coefficients $z_n^m$ uniquely describes the wave front. Since the polynomials are orthogonal, the cumulative RMS wave front error is given by the Euclidian norm of the vector $z$:
$‖z‖_2=\sqrt{\sum z^2}$
Since the modes are orthogonal, they are mutually independent. Expanding the approximation with higher order terms does not influence the coefficients of the lower order terms.
Deformable mirror
Zernike polynomials are often used in beam optics, since they represent common optical aberrations. For instance, the first three modes (piston, tip & tilt) represent the orientation of an optical component in the system, and by manipulating the $Z_2^0$ mode, the focus of a system can be controlled.
At JPE we use Zernike polynomials in our Cryogenic “Set-and Forget” Deformable Mirror. Optical components like lenses and mirrors create static aberrations in the wave front due to manufacturing and alignment tolerances. These errors can only be measured once the system is installed. Infrared systems are cooled down to cryogenic temperatures, making the access to iterative re-alignment very difficult.
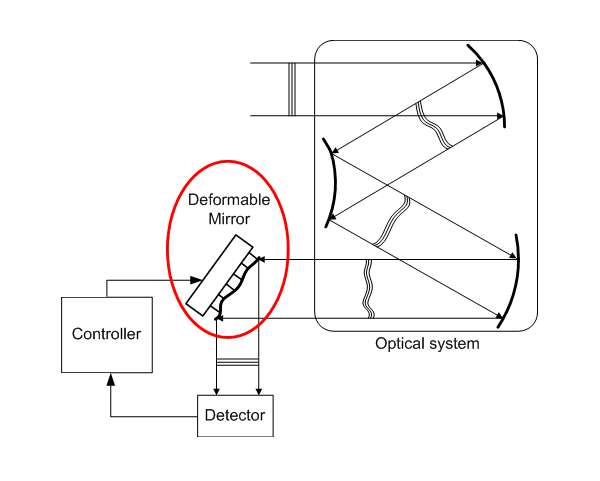
A detector measures the shape of the wave front error and a controller determines the first 15 Zernike coefficients. The required surface shape of the deformable mirror is determined. Cryo Linear Actuators are used to deform the mirror surface and correct the wave front error. Once the desired shape is reached, the actuators lock on friction and do not dissipate any energy.
