Introduction
2 Elastic hinges or flexure hinges in parallel form a reinforced leaf spring and can be used in monolithic structures to be able to have relative motion or displacement. This sheet elaborates on the design of these flexure hinges to acquire the desired stiffness for your suspension.
Usage
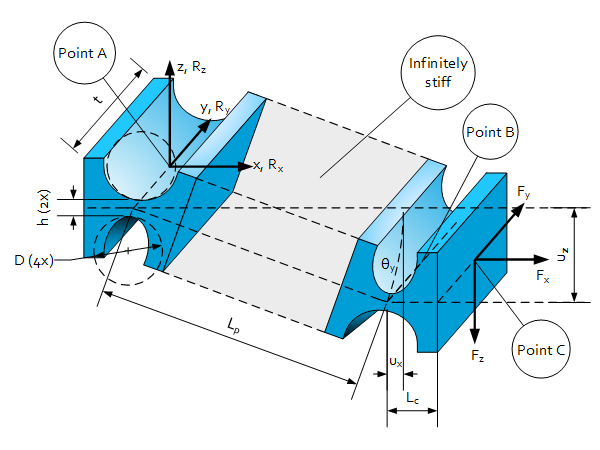
Used as a stiff alternative ($C_x$) for a leaf spring. Note that stiffness in other directions increase as well.
Geometric & motion characteristics
$u_z=\frac{F_z}{C_{Bz}}$
$u_x^*=\frac{1}{2}\cdot\frac{u_z^2}{L_P}$
* s-shape and if $u_z\ll L$
$\theta_y^{\ast\ast}\approx\frac{u_z}{L}$
** s-shape and if $u_z\ll L$
Stiffness at point C
For the stiffness of a single elastic hinge at point A see sheet Flexure hinge or elastic hinge
$C_{Cx}=\frac{C_{Ax}}{2}\approx0.24Et\sqrt{\frac{h}{D}}$
$C_{Cy\left(c-shape\right)}\approx\frac{K_{Az}}{\left(L_p+L_c\right)^2+{L_c}^2\ }=\frac{0.04Et^3\sqrt{\frac{h}{D}}}{\left(L_p+L_c\right)^2+{L_c}^2}$
Note: for deformation in Y-direction the stiffness $C_{Ay}$ is assumed to be infinite.
$C_{Cz\left(s-shape\right)}\approx\frac{2K_{Ay}}{L_p^2\ }=\frac{0.186Eth^2\sqrt{\frac{h}{D}}}{L_p^2} $
Note: for deformation in Z-direction the stiffness $C_{Az}$ is assumed to be infinite.
Stress
Determinative for the stroke $\theta_y$:
$\sigma_{max}^*=0.58E\sqrt{\frac{h}{D}}\cdot\theta_y$
* s-shape