Introduction
3 parallel & tangential folded leaf springs are often used as a z, Rx, Ry fixation. Each leaf spring contributes to the total stiffness of the setup. This sheet describes the stiffness and stroke of the individual and the combination of 3 parallel & tangential folded leaf springs @ 120º.
Individual stiffness
The stiffness varies with the angle θ. If the leaf spring is combined with others the following holds*.
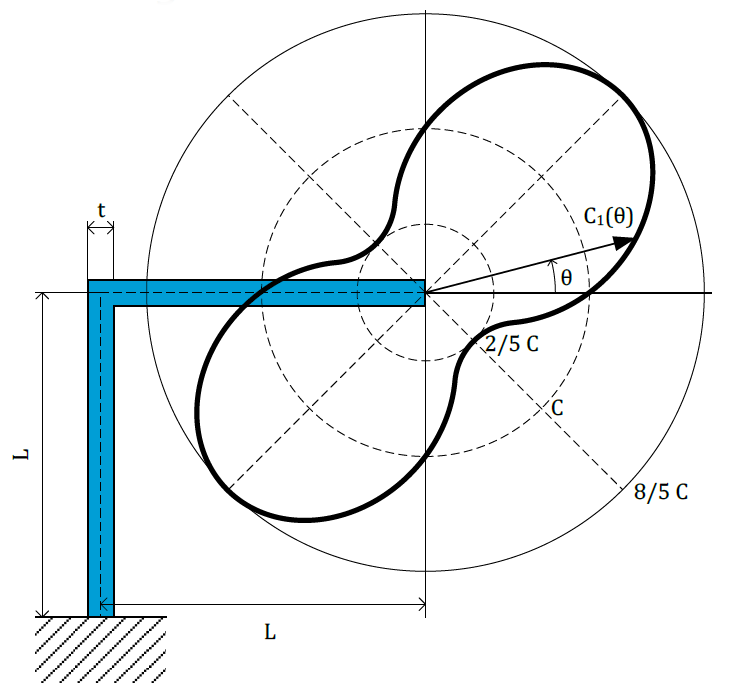
Angle dependent linear stiffness:
$C_{t1}(\theta)\ =C\left(1+\frac{3}{5}\sin{\left(2\theta\right)}\right)$
With: $C=\frac{15}{2}\frac{EI}{L^3} $
Linear stiffness perpendicular to drawing:
$C_{z1}=\frac{Etb^3}{\left(2L\right)^3+2b^2(2L)(1+\nu)}$
* If a folded leaf spring is used individually, the stiffness varies according to some boundary conditions, see Flexure engineering fundamental: Folded leaf spring.
Individual stroke
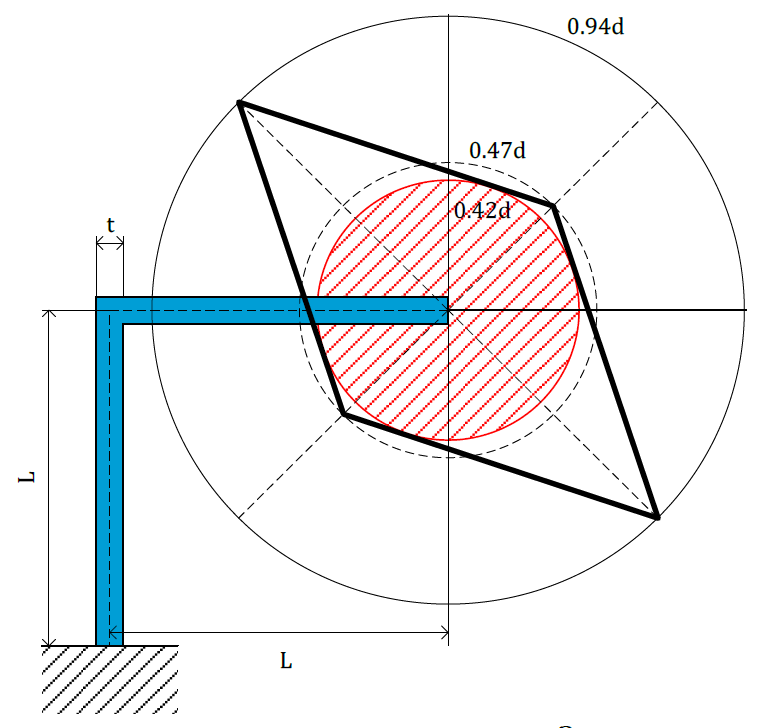
Stiff direction:
Compliant direction:
Unidirectional:
$\delta_{stiff}=\frac{2}{3\sqrt2}d\approx0.47d$
$\delta_{compl}=\frac{4}{3\sqrt2}d\approx0.94d$
$\delta_{uni}\le0.42d$
With $d=\frac{\sigma L^2}{Et}$
Combined leaf springs @ 120º
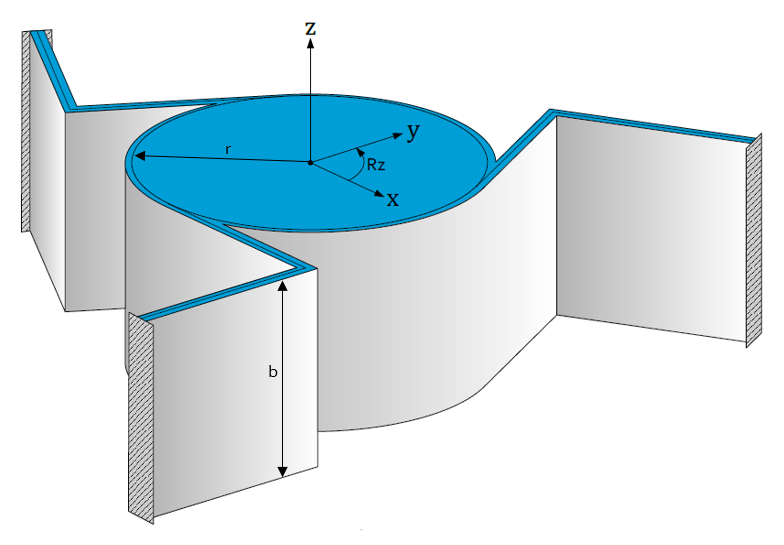
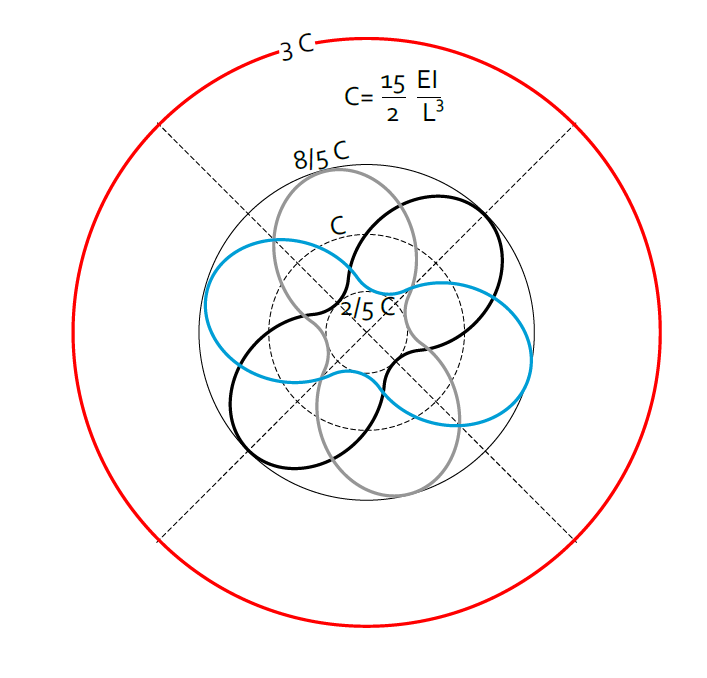
Combined Stiffness
Angle dependent stiffness of the folded leaf springs:
$C_{t1}(\theta)\ =C\left(1+\frac{3}{5}\sin{\left(2\theta\right)}\right)$
$C_{t2}(\theta)\ =C\left(1+\frac{3}{5}\sin{\left(2\theta+\frac{2}{3}\pi\right)}\right)$
$C_{t3}(\theta)\ =C\left(1+\frac{3}{5}\sin{\left(2\theta-\frac{2}{3}\pi\right)}\right)$
Combined radial stiffness:
$C_{radial}=C_{t1}\left(\theta\right)+C_{t2}\left(\theta\right)+C_{t3}\left(\theta\right)=3\cdot C=\frac{45}{2}\frac{EI}{L^3}$
Combined linear z-stiffness:
$C_{axial}=3C_{z1}=\frac{3}{2}\frac{Etb^3}{L^3}$
Combined rotational stiffness:
$K_x=K_y=C_{axial}\cdot r^2=\frac{3}{2}\frac{Etb^3r^2}{L^3}$
$K_z=\left(C_{t1}\left(\theta\right)+C_{t2}\left(\theta+120^{\circ}\right)+C_{t3}\left(\theta-120^{\circ}\right)\right)\cdot r^2=\frac{45}{2}\frac{EIr^2}{L^3}$
Combined stroke
$\delta_{uni}\le0.42\cdot d=0.42\frac{\sigma L^2}{Et}$
Note that in the stiff direction of 1 folded leaf spring, the other is not stiff, so only the unidirectional stroke can be used.
