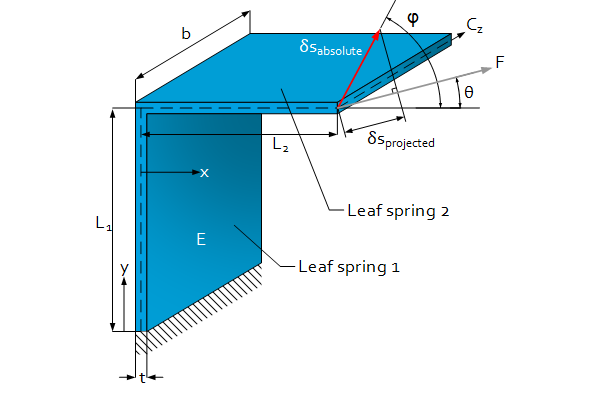
Introduction
Folded leaf springs can be used for stiffness in one direction as an alternative for a rod.
Pro’s & Con’s
- No parasitic displacements
- Force (grey arrow) and displacement (red arrow) are not unidirectional. To obtain an identical direction an additional guiding is necessary and thus ‘extra stiffness’ is introduced.
Equations folded leaf spring with free end
$F_x=F\cdot cos\left(\theta\right)$
$F_y=F\cdot sin\left(\theta\right)$
$I=\frac{1}{12}bt^3$
$\delta s_{x\ at\ \theta}=\frac{L_1^2}{EI}\left(\frac{1}{3}F_xL_1-\frac{1}{2}F_yL_2\right)$
$\delta s_{y\ at\ \theta}=\frac{L_2}{EI}\left(\frac{1}{3}F_yL_2^2+F_yL_1L_2-\frac{1}{2}F_xL_1^2\right)$
$\delta s_{absolute\ at\ \theta}=\sqrt{\delta s_y^2+\delta s_x^2}$
$\delta s_{projected\ at\ \theta}=\delta s_{absolute}\cdot\cos{\left(\theta-\varphi\right)} $
$C_{absolute\ at\ \theta}=\frac{F}{\delta s_{absolute}}$ (bidirectional)
$C_{projected\ at\ \theta}=\frac{F}{\left|\delta s_{projected}\right|}$ (unidirectional)
Moment & Stress
$M_{vertical\ beam}\left(y\right)=F_xL_1-F_yL_2-F_xy $
$M_{horizontal\ beam}(x)=F_yL_2-F_yx$
$\sigma_{max}=\frac{\left|M_{max}\right|\frac{1}{2}t}{I}$
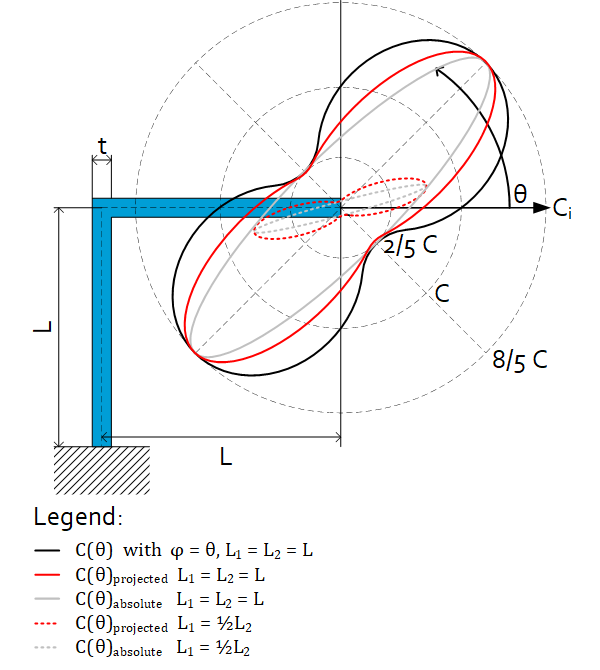
Common case: $L_1=\ L_2=L$
$\delta\ s_{x\ at\ \theta}=\frac{L^3}{EI}\left(\frac{1}{3}F_x-\frac{1}{2}F_y\right)$
$\delta\ s_{y\ at\ \theta}=\frac{L^3}{EI}\left(\frac{4}{3}F_y-\frac{1}{2}F_x\right)$
Guided case: $\varphi=\theta$ and $L_1=\ L_2=L$
$C=\frac{15}{2}\frac{EI}{L^3} $
$C_{at\ \theta}\ =C\left(1+\frac{3}{5}\sin{\left(2\theta\right)}\right) $
Stiffness of folded leaf spring in stiff direction (all cases)
$C_z=\frac{1}{\frac{1}{C_b}\ +\ \frac{1}{C_s}}=\frac{Etb^3}{\left(L_1+L_2\right)^3+2b^2(L_1+L_2)(1+\nu)}$
$C_b=\frac{Etb^3}{\left(L_1+L_2\right)^3}$ (bending)
$C_s=\frac{Ebt}{2\left(1+\nu\right)(L_1+L_2)}$ (shear)
Note: this is under the assumption that at $C_z$ the rotations are fixed, which is common in a 3 parallel & tangential folded leaf springs configuration. Torsion of leaf spring 1 is also not taken into consideration.
Stiffness graph