Introduction
For slender structures there is a risk that buckling may occur when loaded with compression. This sheet gives the force at which buckling occurs ($F_b$) for beams with various boundary constraints. For more information on buckling see the page Buckling fundamentals.
Buckling of uniform beams / leaf springs
The buckling force is given by:
$$F_b=\frac{\pi^2EI_x}{L_b^2}$$
With $L_b$ denoting the representative buckling length of the beam given by the table below, $E$ indicates the Young’s modulus of the material and $I_x$ indicates the area moment of inertia. For more information on, and calculations of the area moment of inertia $I_x$, see page: Area moment of inertia.
The buckling length of a beam is the buckling coefficient times the length of the beam. The buckling coefficient is dependent on the load case. A lower buckling coefficient means that the load case is more resistant to buckling.
| Load case | $L_b$ | Load case | $L_b$ |
|---|---|---|---|
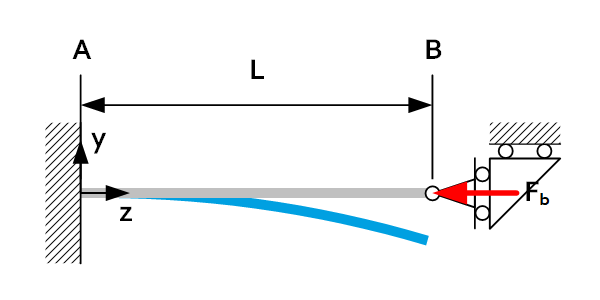 | 2L | 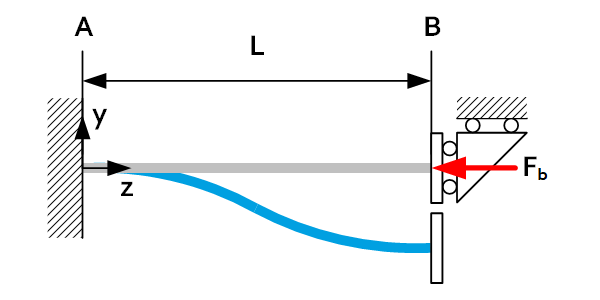 | 1L |
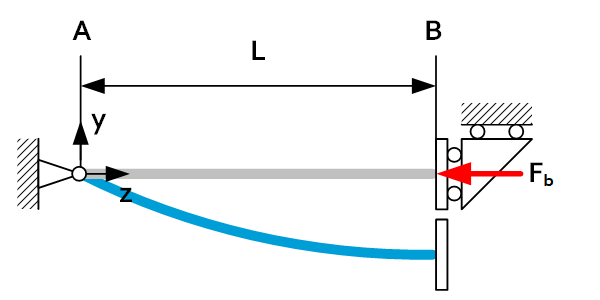 | 2L | 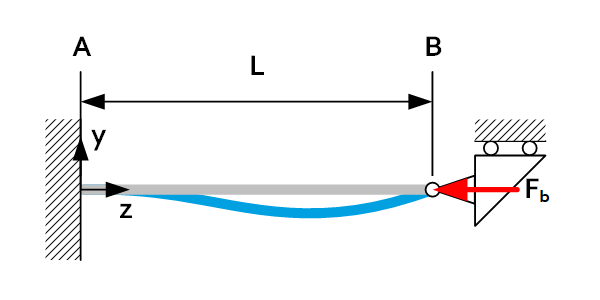 | 0.7L |
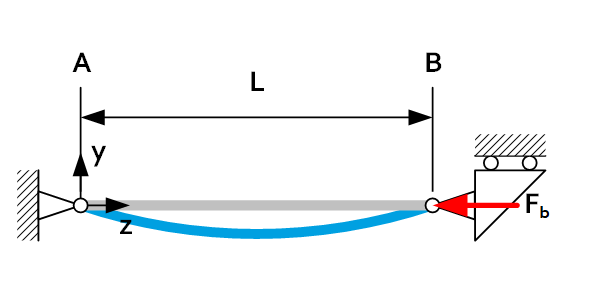 | 1L | 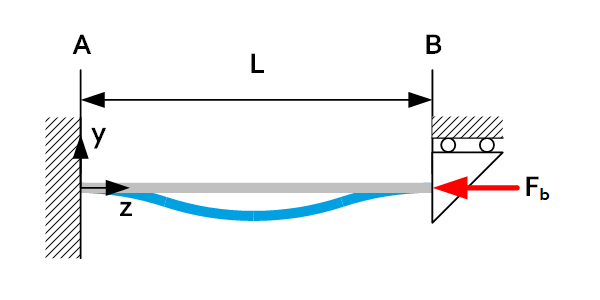 | 0.5L |
Buckling of reinforced beams / leaf springs
By reinforcing the mid-section of a beam its buckling force will be greatly increased while keeping the lateral stiffness and maximum bending stress approximately the same. For two common load cases the buckling force equations are shown below.
For this case, $I_{xs}$ indicates the area moment of inertia of the thin section.
| Load case | $F_b/L_b$ | Load case | $F_b/L_b$ |
|---|---|---|---|
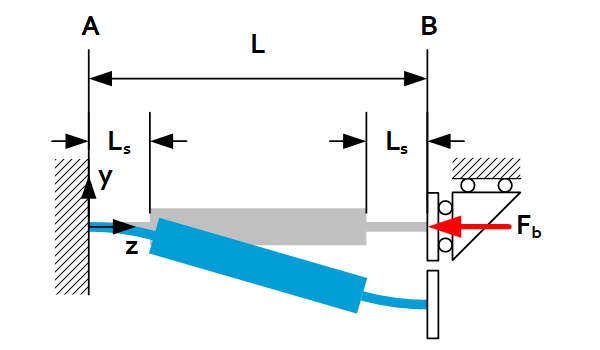 | $$F_b=\frac{\pi^2EI_{xs}}{4L_sL}$$ or $$L_b=2\sqrt{L_sL}$$ | 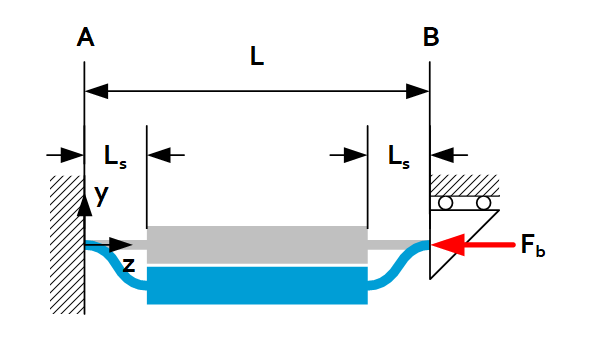 | $$F_b=\frac{\pi^2EI_{xs}}{L_s^2}$$ or $$L_b=L_s$$ |
