Introduction
Flexures or leaf springs can be used for play and friction free motion. A downside is stiffness and to minimize the needed force, the flexures are made slender and thin. Smart reinforcement of flexures and leaf springs can help to keep the needed motion-force minimal while the flexure or leaf spring is made thicker, which is beneficial for its carrying stiffness and easier to manufacture which will decrease the manufacturing costs.
Design parameters
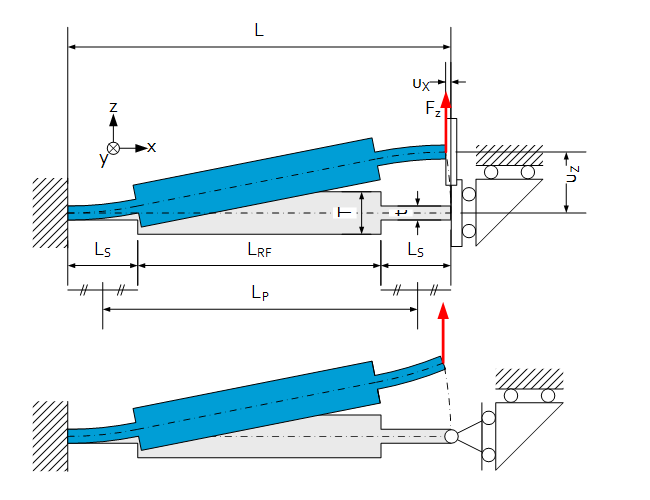
$\lambda=\frac{L_s}{L}$
$0<\lambda<\frac{1}{2}$
$L_P=L_{RF}+L_s=\left(1-\lambda\right)L$
$\gamma=\frac{t}{T}$
$0<\gamma<1$
Deformation characteristics
$u_z=\frac{F_z}{C_z} $
$u_x=\frac{u_z^2}{2L\left(1-\lambda\right)}$ (s-shape deformation)
Stiffness for s- and c-shape deformation
$C_x=\frac{1}{2\lambda\left(1-\gamma\right)+\gamma}\cdot\frac{Etb}{L}$
$C_y=\frac{1}{2\lambda\left(4\lambda^2-6\lambda+3\right)\left(1-\gamma\right)+\gamma}\cdot\frac{Etb^3}{L^3}$ (s-shape deformation)
$C_y=\frac{1}{2\lambda\left(4\lambda^2-6\lambda+3\right)\left(1-\gamma\right)+\gamma}\cdot\frac{Etb^3}{4L^3}$ (c-shape deformation)
$C_z=\frac{1}{2\lambda\left(4\lambda^2-6\lambda+3\right)\left(1-\gamma^3\right)+\gamma^3}\cdot\frac{Ebt^3}{{L}^3}$ (s-shape deformation)
$C_z=\frac{1}{2\lambda\left(4\lambda^2-6\lambda+3\right)\left(1-\gamma^3\right)+\gamma^3}\cdot\frac{Ebt^3}{4{L}^3}$ (c-shape deformation)
$K_x=\frac{1}{2\lambda\left(1-\gamma^3\right)+\gamma^3}\cdot\frac{Gbt^3}{3L}$
$K_y=\frac{1}{2\lambda\left(1-\gamma^3\right)+\gamma^3}\cdot\frac{Ebt^3}{12L}$ (c-shape deformation)
$K_z=\frac{1}{2\lambda\left(1-\gamma\right)+\gamma}\cdot\frac{Etb^3}{12L}$ (c-shape deformation)
Force limits (buckling)
Design guidelines
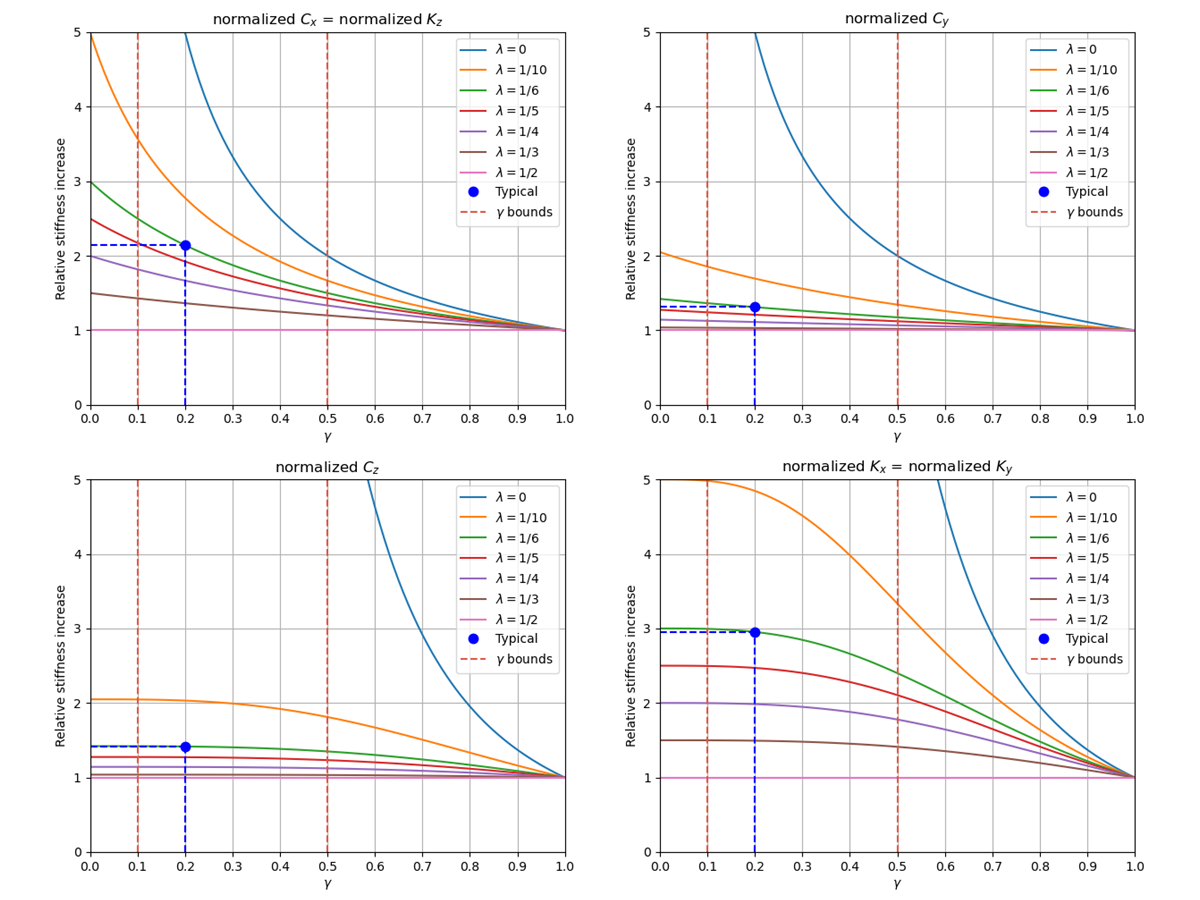
Keep $\frac{1}{10}<\lambda<\frac{1}{3}$ and $\frac{1}{10}<\gamma<\frac{1}{2}$
Typical $\lambda=\frac{1}{6}$ and $\gamma=\frac{1}{5}$
Then:
$C_x=2.1\cdot\frac{Etb}{L}$
$C_y=1.3\cdot\frac{Etb^3}{L^3}$ (s-shape / c-shape)
$C_z=1.4\cdot\frac{Ebt^3}{L^3}$ (s-shape / c-shape)
$K_x=3.0\cdot\frac{Gbt^3}{3L}$
$K_y=3.0\cdot\frac{Ebt^3}{12L}$ (c-shape)
$K_z=2.1\cdot\frac{Etb^3}{12L}$ (c-shape)
Normalized stiffness increase due to reinforcement
The graphs shown below indicate the normalized stiffness increase with respect to the non-reinforced case ($\lambda=0.5$).