Reinforced strut

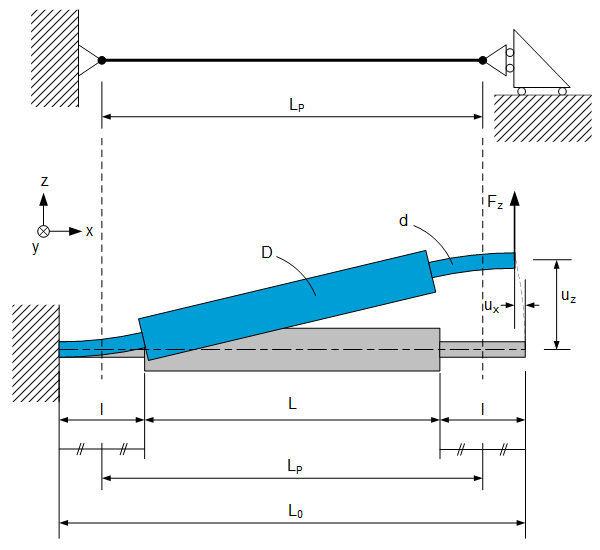
Introduction

Struts are often used for connecting two bodies in 1 DOF (x), while keeping the other DOFs free. In many cases the function of a stiff element with two hinges is desired. This is achieved by reinforcing the midsection of the strut. The poles of the hinges are located at the center of the thin sections, so to keep the same motion profile the strut length increases slightly. The buckling force is increased significantly, while the remaining stiffness in the motion directions is kept relatively unchanged.

In theory the midsection has 5 unconstrained DOFs, which leads to internal resonances. This can affect the controllability of the mechanism in high frequency applications.

Design parameters

$\lambda=\frac{l}{L_P}$,     $ \gamma=\frac{d}{D}$

$L_P=L+l$
$L_0=L+2l$

Deformation characteristics

$u_z=\frac{F_z}{C_z} $
$u_x\approx\frac{{-u}_z^2}{2L_P}$

Stiffness

$C_x=\frac{1}{\gamma^2+2\lambda}\cdot\frac{E\pi d^2}{4L_P}\ $
$C_y=C_z=\frac{1}{6\lambda}\cdot\frac{3E\pi d^4}{16L_P^3} $
$K_x=\frac{1}{2\lambda}\cdot\frac{G\pi d^4}{32L_P} $
$K_y=K_z=\frac{1}{2\lambda}\cdot\frac{E\pi d^4}{64L_P} $

Stress

$\sigma_{max}=\left(1+\lambda\right)\cdot\frac{16L_PF_z}{\pi d^3} $

Force limits

The maximum transverse force is:

$F_{z,max}=\frac{\sigma_y\pi d^3}{16L_P(1+\lambda)}$

When a force in x-direction is applied buckling can occur, for equations to calculate the buckling load see Beam Theory: Buckling.

Maximum deflection

$u_{z,max}=\frac{F_{z,max\ }}{C_z}=\frac{\left(8\lambda^3-12\lambda^2+6\lambda\right)\left(1-\gamma^4\right)+\gamma^4}{\left(1+\lambda\right)}\cdot\frac{\sigma_yL_P^2}{3Ed} $