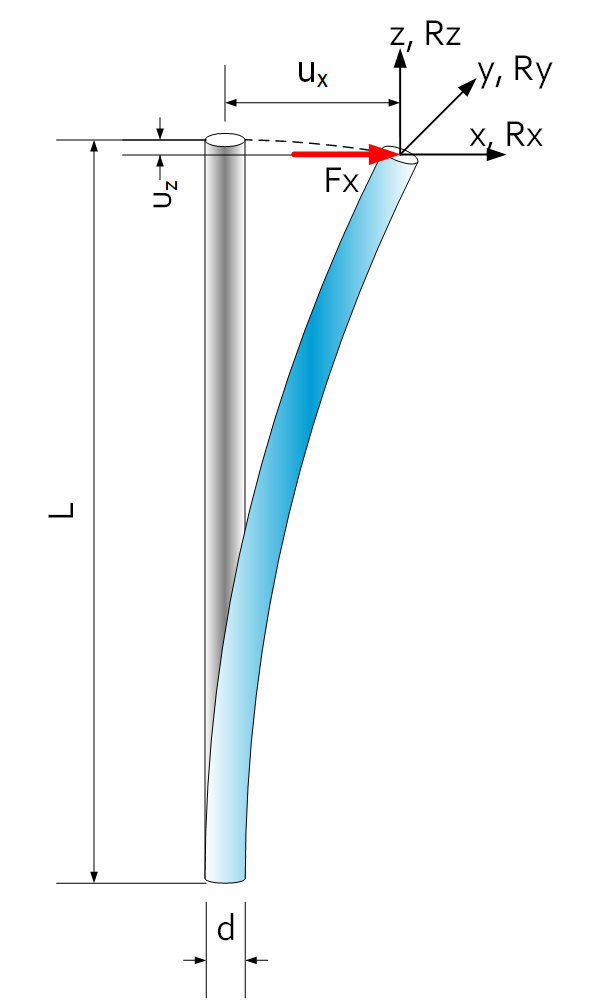
S-shape stiffness
$C_x=C_y=\frac{12EI}{L^3}=\frac{3\pi E\ d^4}{16L^3}$
$C_z=\frac{EA}{L}$ only if $u_x=0$
$C_z=\frac{1}{\frac{L}{EA}+\frac{u_x^2L}{700EI}}$ for $u_x\neq0$
$K_x=K_y=\frac{EI}{L}=\frac{\pi E\ d^4}{64L}$
$K_z=\frac{G{\pi d}^4}{32L}=\frac{E{\pi d}^4}{64\left(1+\nu\right)L}$
S-shape motion characteristics
$u_x=\frac{F_x}{C_x}$
$u_{xmax}=\frac{1}{3}\frac{L^2}{Ed}\sigma_{max}$
$u_z=\frac{3}{5}\frac{u_x^2}{L}$
S-shape force limits
$\sigma_{max}=\frac{M_{max}}{I}\frac{1}{2}d=\frac{\frac{F_xL}{2}}{I}\frac{1}{2}d=\frac{F_xLd}{4I}$
dynamic movements: $\sigma_{max}<$ fatigue stress limit
static deformation: $\sigma_{max}<$ yield stress limit $(\sigma_{0.2})$
See Beam Theory: Buckling for equations to calculate the maximum buckling load.

C-shape stiffness
$C_x=C_y=\frac{3EI}{L^3} $
$C_z=\frac{EA}{L}$ only if $u_x=0$
$K_x=K_y=\frac{EI}{L}=\frac{\pi E\ d^4}{64L}$
$K_z=\frac{G{\pi d}^4}{32L}=\frac{E{\pi d}^4}{64\left(1+\nu\right)L}$
C-shape motion characteristics
$u_x=\frac{F_x}{C_x}$
$u_{xmax}=\frac{2}{3}\frac{L^2}{Ed}\sigma_{max}$
$u_z=\frac{3}{5}\frac{u_x^2}{L}$
C-shape force limits
$\sigma_{max}=\frac{M_{max}}{I}\frac{1}{2}d=\frac{F_xL}{I}\frac{1}{2}d=\frac{F_xLd}{2I}$
dynamic movements: $\sigma_{max}<$ fatigue stress limit
static deformation: $\sigma_{max}<$ yield stress limit $(\sigma_{0.2})$
See Beam Theory: Buckling for equations to calculate the maximum buckling load.